Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(\left|z\right|=\sqrt{\left(1+\cos a\right)^2+\sin^2a}=\sqrt{2\left(1+\cos a\right)}=\sqrt{4\cos^2\frac{a}{2}}=2\left|\cos\frac{a}{2}\right|\)
a) Nếu \(a\in\left(0,\pi\right)\Rightarrow\frac{a}{2}\in\left(0,\frac{\pi}{2}\right)\), P nằm góc phần tư thứ nhất.
Do đó
\(\theta=arctan\frac{\sin a}{1+\cos a}=arctan\left(tan\frac{a}{2}\right)=\frac{a}{2}\)
\(z=2\cos\frac{a}{2}\left(\cos\frac{a}{2}+i\sin\frac{a}{2}\right)\)
b)
Nếu \(a\in\left(\pi,2\pi\right)\Rightarrow\frac{a}{2}\in\left(\frac{\pi}{2},\pi\right)\), P nằm góc phần tư thứ tư.
Do đó
\(\theta=arctan\left(tan\frac{a}{2}\right)+2\pi=\frac{a}{2}-\pi+2\pi=\frac{a}{2}+\pi\)
\(z=-2\cos\frac{a}{2}\left[\cos\left(\frac{a}{2}+\pi\right)+i\sin\left(\frac{a}{2}+\pi\right)\right]\)
c) Nếu \(a=\pi\) thì \(z=0\)
Chọn C
Ta có: 
nên (1) và (2) có nghiệm.
Cách 1:
Xét: 
nên (3) vô nghiệm.
Cách 2:
Điều kiện có nghiệm của phương trình: sin x + cos x = 2 là: 
(vô lý) nên (3) vô nghiệm.
Cách 3:
Vì 
nên (3) vô nghiệm.
Gọi \(P_1,P_2\) là giao điểm của đường tròn (0.1) với tia OM1 và OM2
Dựng P3 thuộc đường tròn và có argument cực \(\theta_1,\theta_2\) Chọn M3 thuộc tia OP3, OM3 =OM1.OM2
Gọi z3 là tọa độ phức của M3. Điểm M3(\(r_1r_2;\theta_1+\theta_2\) biểu diễn tích z1z2
Gọi A là điểm biểu diễn của z=1
\(\frac{OM_3}{OM_1}=\frac{OM_2}{1}\Rightarrow\frac{OM_3}{OM_2}=\frac{OM_2}{OA};\widehat{M_2OM_3}=\widehat{AOM_1}\)
Suy ra 2 tam giác OAM1 và OM2M3 đồng dạng
nhaans máy tính là được mà. chuyển về chế độ radian bạn nà
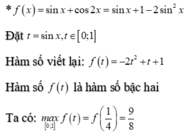
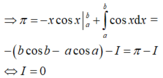
Chọn C
Ta có: