Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do hàm số y = f(x) nghịch biến trên khoảng (a;b) nên
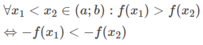
Vậy hàm số y = - f(x) đồng biến trên khoảng (a;b).

a: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-6}{2\cdot4}=\dfrac{-6}{8}=\dfrac{-3}{4}\\y=-\dfrac{6^2-4\cdot4\cdot\left(-5\right)}{4\cdot4}=-\dfrac{29}{4}\end{matrix}\right.\)
Bảng biến thiên là:
| x | -\(\infty\) -3/4 +\(\infty\) |
| y | -\(\infty\) -29/4 +\(\infty\) |

b: Hàm số đồng biến khi x>-3/4; nghịch biến khi x<-3/4
GTNN của hàm số là y=-29/4 khi x=-3/4

a: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-10}{2\cdot\left(-3\right)}=\dfrac{10}{6}=\dfrac{5}{3}\\y=-\dfrac{10^2-4\cdot\left(-3\right)\cdot\left(-4\right)}{4\cdot\left(-3\right)}=\dfrac{13}{3}\end{matrix}\right.\)
Bảng biến thiên:
| x | -\(\infty\) 5/3 +\(\infty\) |
| y | +\(\infty\) 13/3 -\(\infty\) |

b: Hàm số đồng biến khi x<5/3; nghịch biến khi x>5/3
Giá trị nhỏ nhất là y=13/3 khi x=5/3

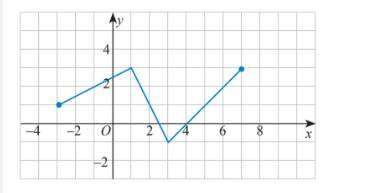
a) Từ đồ thị ta thấy hàm số xác định trên [-3;7]
+) Trên khoảng (-3; 1): đồ thị có dạng đi lên từ trái sang phải nên hàm số này đồng biến trên khoảng (-3; 1).
+) Trên khoảng (1; 3): đồ thị có dạng đi xuống từ trái sang phải nên hàm số này nghịch biến trên khoảng (1; 3).
+) Trên khoảng (3; 7): đồ thị có dạng đi lên từ trái sang phải nên hàm số này đồng biến trên khoảng (3; 7).
b) Xét hàm số \(y = 5{x^2}\) trên khoảng (2; 5).
Lấy \({x_1},{x_2} \in (2;5)\) là hai số tùy ý sao cho \({x_1} < {x_2}\).
Do \({x_1},{x_2} \in (2;5)\) và \({x_1} < {x_2}\) nên \(0 < {x_1} < {x_2}\), suy ra \({x_1}^2 < {x_2}^2\) hay \(5{x_1}^2 < 5{x_2}^2\)
Từ đây suy ra \(f({x_1}) < f({x_2})\)
Vậy hàm số đồng biến (tăng) trên khoảng (2; 5).

1.
Vì \(y=\sqrt{2}\) là hàm hằng nên với mọi giá trị của \(x\) thì đều nhận \(\sqrt{2}\) là giá rị của \(y\)
\(\Rightarrow B\)
2. \(D\)
3.
Giải hệ \(\left\{{}\begin{matrix}\dfrac{1}{2}\left(x+2\right)\left(y+3\right)=\dfrac{1}{2}xy+50\\\dfrac{1}{2}\left(x-2\right)\left(y-2\right)=\dfrac{1}{2}xy-32\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=26\\y=8\end{matrix}\right.\)
\(\Rightarrow xy=208\Rightarrow A\)
4.
\(\overrightarrow{AM}.\overrightarrow{AN}=-a^2\)
5.
\(\left[{}\begin{matrix}m=\dfrac{5}{2}\\m=-\dfrac{7}{2}\end{matrix}\right.\)
6. \(C\)
Câu 4: Đáp án
A. \(2a^2\) B.\(a^2\) C.\(\frac{1}{2}a^2\) D.\(\frac{-1}{2}a^2\)
Không có đáp án \(-a^2 \)
Đáp án A