
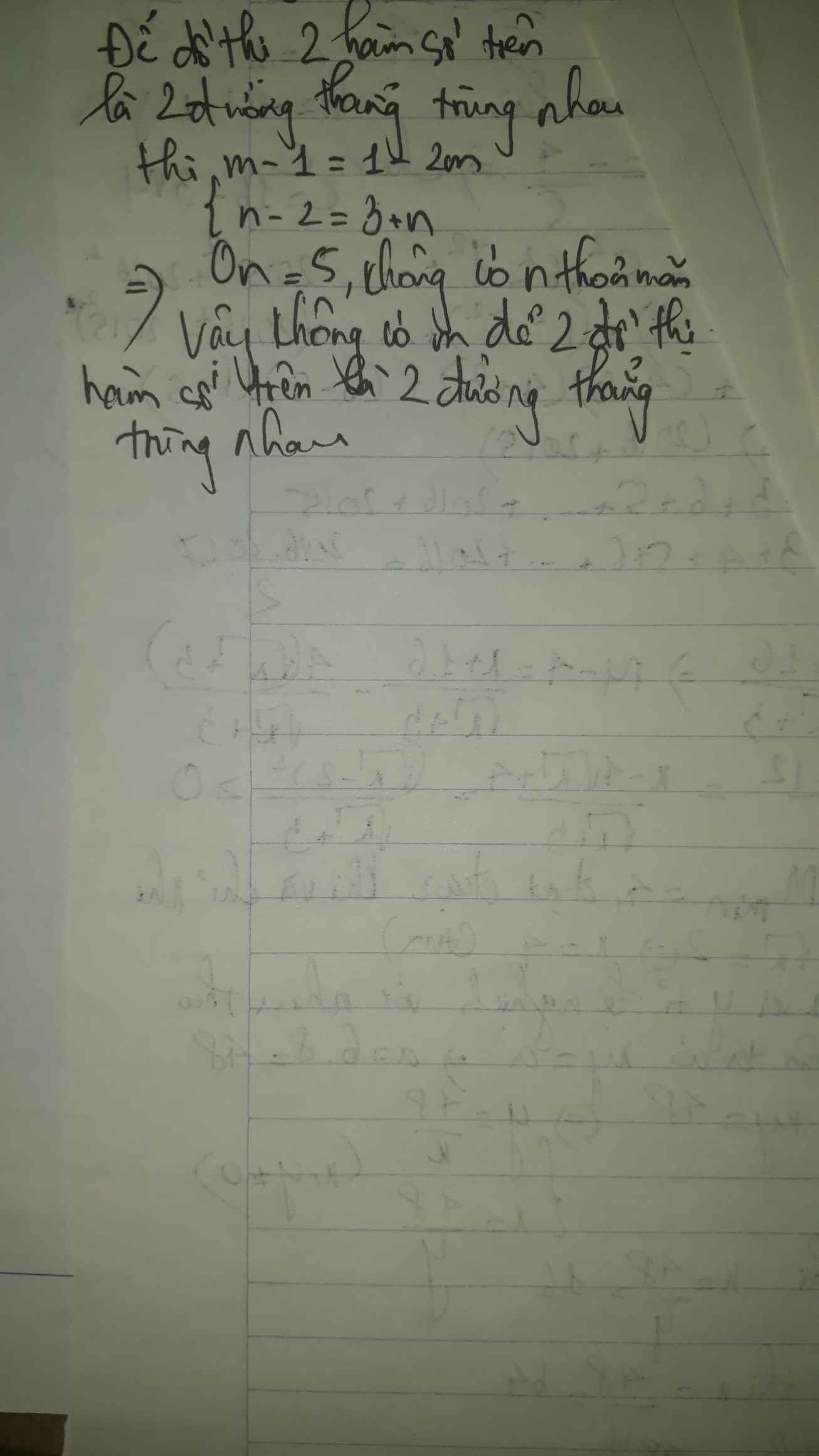
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

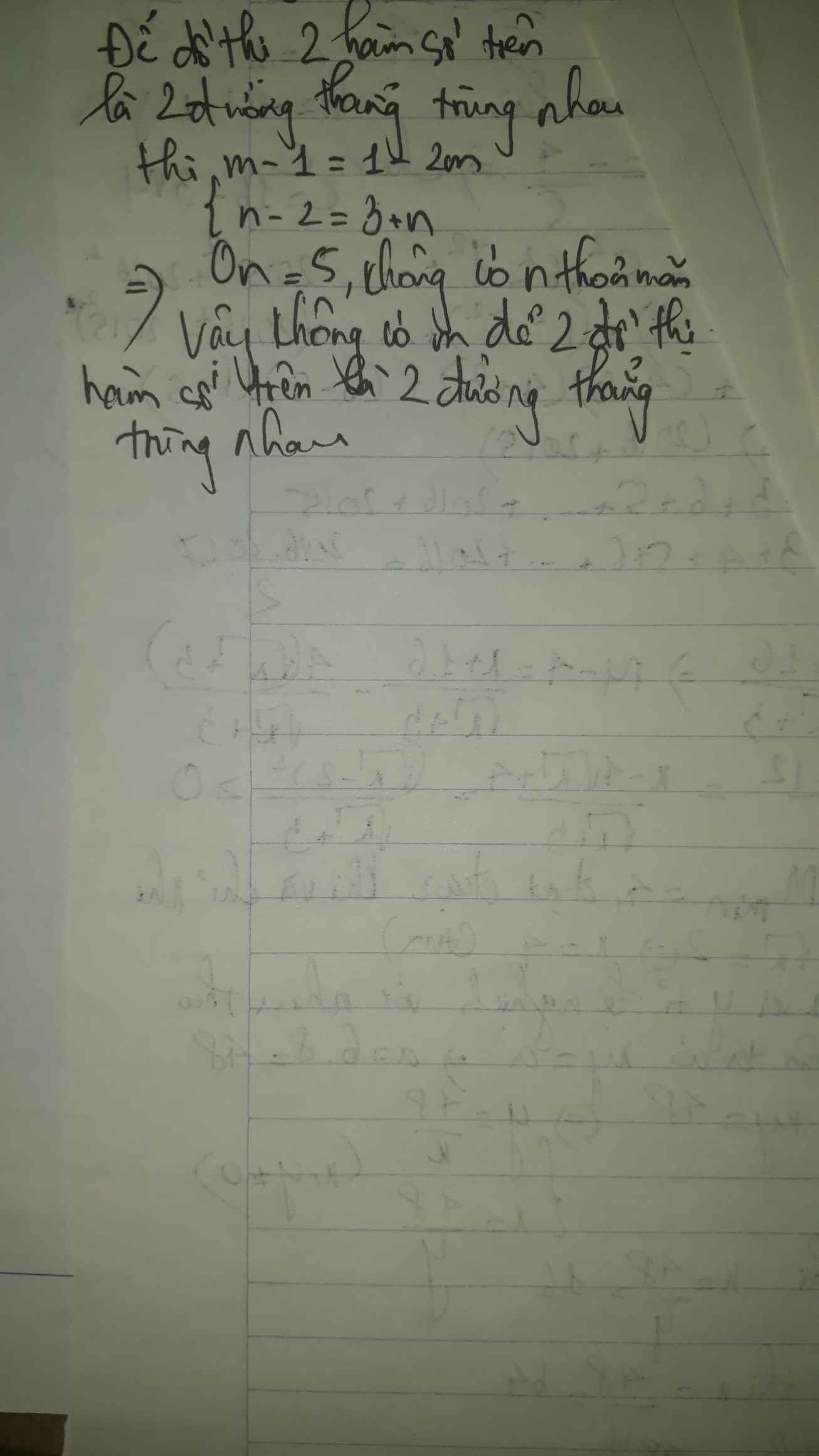

Bài 1:
Đặt: (d): y = (m+5)x + 2m - 10
Để y là hàm số bậc nhất thì: m + 5 # 0 <=> m # -5
Để y là hàm số đồng biến thì: m + 5 > 0 <=> m > -5
(d) đi qua A(2,3) nên ta có:
3 = (m+5).2 + 2m - 10
<=> 2m + 10 + 2m - 10 = 3
<=> 4m = 3
<=> m = 3/4
(d) cắt trục tung tại điểm có tung độ bằng 9 nên ta có:
9 = (m+5).0 + 2m - 10
<=> 2m - 10 = 9
<=> 2m = 19
<=> m = 19/2
(d) đi qua điểm 10 trên trục hoành nên ta có:
0 = (m+5).10 + 2m - 10
<=> 10m + 50 + 2m - 10 = 0
<=> 12m = -40
<=> m = -10/3
(d) // y = 2x - 1 nên ta có:
\(\hept{\begin{cases}m+5=2\\2m-10\ne-1\end{cases}}\) <=> \(\hept{\begin{cases}m=-3\\m\ne\frac{9}{2}\end{cases}}\) <=> \(m=-3\)

a: Để hai đường thẳng song song thì \(\left\{{}\begin{matrix}m-1=1-2m\\n-2\ne n+3\end{matrix}\right.\Leftrightarrow3m=2\Leftrightarrow m=\dfrac{2}{3}\)
b: Để hai đường thẳng cắt nhau thì \(m-1\ne-2m+1\)
\(\Leftrightarrow3m\ne2\)
hay \(m\ne\dfrac{2}{3}\)

Để hai đồ thị này song song thì
\(\left\{{}\begin{matrix}2m+4=m-1\\n< >2n-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m=-5\\n< >2\end{matrix}\right.\)

Hai đường thẳng trùng nhau khi a = a' và b = b' tức là:
2 = 2m + 1 và 3k = 2k – 3
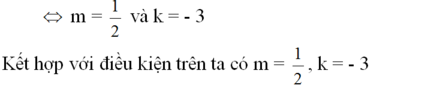

Trả lời :
Bn Do Phuong Mai đừng bình luận linh tinh nhé !
- Hok tốt !
^_^