Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

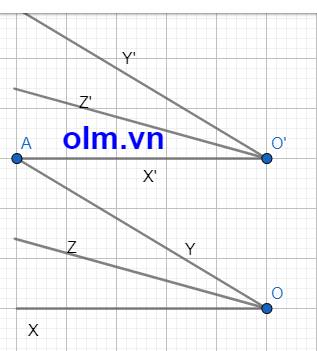
a,Kéo dài OY cắt O'X' tại A ta có:
\(\widehat{XOY}\) = \(\widehat{XOA}\) = \(\widehat{OAO'}\) (so le trong) (1)
\(\widehat{Y'O'X'}\) = \(\widehat{Y'O'A}\) = \(\widehat{OAO'}\) (so le trong) (2)
Kết hợp (1) Và (2) ta có:
\(\widehat{XOY=}\) \(\widehat{X'O'Y'}\) (đpcm)
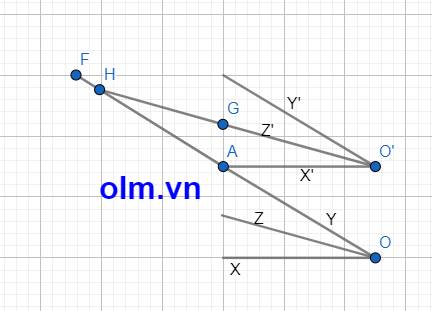
b, Kéo dài OY cắt O'Z' tại H
\(\widehat{ZOA}\) = \(\dfrac{1}{2}\) \(\widehat{XOY}\) (vì OZ là phân giác của góc XOY
\(\widehat{HO'A}\) = \(\dfrac{1}{2}\) \(\widehat{X'O'Y'}\) (vì OY là phân giác của góc X'O'Y')
Mặt khác ta có \(\widehat{OAO'}\) = \(\widehat{HO'A}\) + \(\widehat{AHO'}\) (góc ngoài tam giác bằng tổng hai góc trong không kề với nó)
\(\widehat{HO'A}\) = \(\dfrac{1}{2}\) \(\widehat{OAO'}\) ⇒ \(\widehat{AHO'}\) = \(\dfrac{1}{2}\) \(\widehat{OAO'}\) = \(\dfrac{1}{2}\) \(\widehat{XOY}\)
⇒ \(\widehat{ZOA}\) = \(\widehat{AHO'}\) (hai góc này ở vị trí so le trong)
⇒ OZ // O'Z' (đpcm)

Tương tự 6A.
Tính được x O y ^ = 70°, y O z ^ = 40°.
Tính được x O z ^ = 110°, y O z ' ^ = 140° => x O z ^ < y O z ' ^

Ta có:
\(\widehat{xOy}+\widehat{yOz}=150^O\)
\(\rightarrow\widehat{xOy}-\widehat{yOz}=150^o-2\widehat{yOz}\)
\(\rightarrow90^o=150^o-2\widehat{yOz}\)
\(\rightarrow2\widehat{yOz}=60^o\)
\(\rightarrow\widehat{yOz}=30^o\)
\(\rightarrow\widehat{xOy}=150^o-\widehat{yOz}=120^o\)
b)
Ta có: Oz' là tia đối của tia Oz
\(\rightarrow\widehat{xOz'}=180^o-\widehat{xOz}=30^o\)
\(\rightarrow\widehat{xOz'}=\widehat{yOz}\)
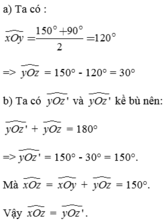
a) Ta có:
x O y ^ = 150 0 + 90 0 2 = 120 0
=> y O z ^ = 150° - 120° = 30°
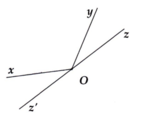
b) Ta có y O z ^ và y O z ' ^ kề bù nên:
y O z ^ + y O z ' ^ = 180°
=> y O z ' ^ = 150° - 30° = 150°.
Mà x O z ^ = x O y ^ + y O z ^ = 150°. Vậy x O z ^ = y O z ' ^ .