Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
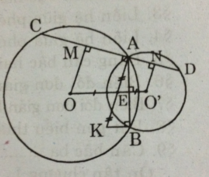
Ta có OO' là đường nối tâm của (O) và (O') nên OO' là đường trung trực của AB.
Suy ra IE ⊥ AB và EA = EB
Ta lại có IA = IK (do K là điểm đối xứng của A qua I).
Nên IE là đường trung bình của tam giác AKB.
Suy ra IE // KB
Mà IE ⊥ AB
Suy ra KB ⊥ AB (đpcm)
b: Gọi giao của AB và OO' là M
=>M là trung điểm của AB và OO' vuông góc với AB tại M
Xét ΔABK có AM/AB=AI/AK
nên MI//BK
=>BK vuông góc với AB
c:
Xét (O) có
ΔABE nội tiếp
AE là đường kính
DO đó: ΔABE vuông tại B
Xet (O') có
ΔABF nội tiếp
AF là đường kính
Do đó; ΔABF vuông tại B
=>BF vuông góc với AB
góc EBF=góc EBA+góc FBA=90+90=180 độ
=>E,B,F thẳng hàng(1)
góc ABE+góc ABK=90+90=180 độ
nên E,B,K thẳng hàng(2)
Từ (1), (2) suy ra E,B,K,F thẳng hàng
mình mới học lớp 7 nhưng chỉ biết câu a sai thì thôi nhé ac=ad vì cái kia = cái này mà cái này = cái kia bạn chỉ cần nói với cô như vậy.Thôi nha
a/ Gọi E, F lần lược là trung điểm của AD, AC
\(\Rightarrow AI\)là đường trung bình của hình thang \(OFEO'\)
\(\Rightarrow AE=AF\)
\(\Rightarrow AD=AC\)
b/ Gọi G là giao điểm của AB với OO'
\(\Rightarrow IG\)là đường trung bình của \(\Delta ABK\)
\(\Rightarrow\)IG // BK
Mà \(IG⊥AB\)
\(\Rightarrow BK⊥AB\)
PS: Bạn vẽ hộ cái hình nhé
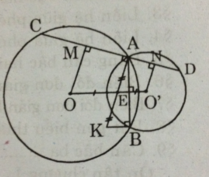Kẻ OM ⊥ AD.
Theo tính chất đường kính vuông góc với một dây, ta có: MA = MC
Tương tự, kẻ O'N ⊥ AD => NA = ND.
Ta có:
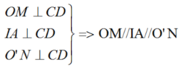
Vậy tứ giác OMNO' là hình thang vuông.
Ta còn có: IO = IO' (gt) và IA // OM
Do đó IA là đường trung bình của hình thang OMNO'.
=> AM = AN hay 2AM = 2AN
Hay AC = CD (đpcm)
b)Chứng minh KB ⊥ AB
-Ta có OO’ là đường nối tâm của (O) và (O’) nên OO’ là đường trung trực của AB.
Suy ra IE ⊥ AB và EA = EB
Ta có IA = IK (do K là điểm đối xứng của A qua I).
Và EA = EB
Vậy IE là đường trung bình của tam giác AKB.
Suy ra IE // KB
Mà IE ⊥ AB
Suy ra KB ⊥ AB (đpcm)
a: Xét tứ giác ODAE có
góc ODA+góc OEA=180 độ
=>ODAE là tứ giác nội tiếp
b: \(AE=\sqrt{\left(3R\right)^2-R^2}=2\sqrt{2}\cdot R\)
\(OI=\dfrac{OE^2}{OA}=\dfrac{R^2}{3R}=\dfrac{R}{3}\)
c: Xét ΔDIK vuông tại I và ΔDHE vuông tại H có
góc IDK chung
=>ΔDIK đồng dạng vơi ΔDHE
=>DI/DH=DK/DE
=>DH*DK=DI*DE=2*IE^2
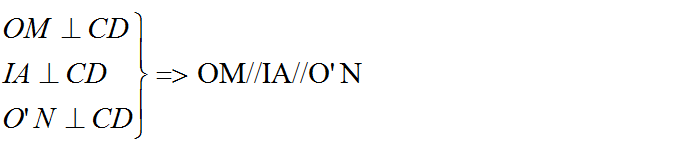
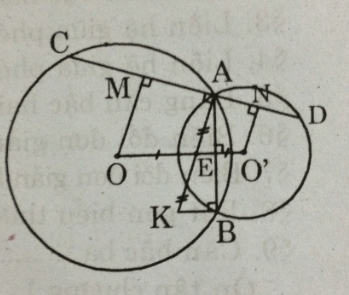
@Thiện Nhân@Thiên Thảo@Guyo@Nguyễn Văn Toàn@Sky SơnTùng
b: Gọi H là giao của AB và OO'
=>OO' vuông góc với AB tại H và H là trung điểm của AB
Xét ΔABK có AH/AB=AM/AK
nên HM//BK
=>BK vuông góc với AB
c: Xét (O) có
ΔABE nội tiếp
AE là đường kính
Do đó: ΔABE vuông tại B
Xét (O') có
ΔAKF nội tiếp
AF là đương kính
Do đó: ΔAKF vuông tại K
Xét (O') có
ΔABF nội tiếp
AF là đường kính
Do đó: ΔABF vuông tại B
góc ABK+góc ABE=90+90=180 độ
=>K,B,E thẳng hàng(1)
góc ABF+góc ABE=90+90=180 độ
nên B,F,E thẳng hàng(2)
Từ (1), (2) suy ra E,B,K,F thẳng hàng
=>OO'//EF
d: Xét ΔAKF có MO'//FK
nên MO'/FK=AO'/AF=1/2
Xét ΔAEK có OM//EK
nên OM/EK=AO/AE=1/2
=>OM/EK=O'M/FK
=>EK=KF
=>K là trung điểm của EF
=>