Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

mình mới học lớp 7 nhưng chỉ biết câu a sai thì thôi nhé ac=ad vì cái kia = cái này mà cái này = cái kia bạn chỉ cần nói với cô như vậy.Thôi nha
a/ Gọi E, F lần lược là trung điểm của AD, AC
\(\Rightarrow AI\)là đường trung bình của hình thang \(OFEO'\)
\(\Rightarrow AE=AF\)
\(\Rightarrow AD=AC\)
b/ Gọi G là giao điểm của AB với OO'
\(\Rightarrow IG\)là đường trung bình của \(\Delta ABK\)
\(\Rightarrow\)IG // BK
Mà \(IG⊥AB\)
\(\Rightarrow BK⊥AB\)
PS: Bạn vẽ hộ cái hình nhé

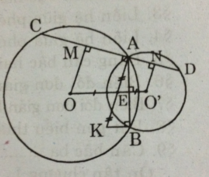
Ta có OO' là đường nối tâm của (O) và (O') nên OO' là đường trung trực của AB.
Suy ra IE ⊥ AB và EA = EB
Ta lại có IA = IK (do K là điểm đối xứng của A qua I).
Nên IE là đường trung bình của tam giác AKB.
Suy ra IE // KB
Mà IE ⊥ AB
Suy ra KB ⊥ AB (đpcm)

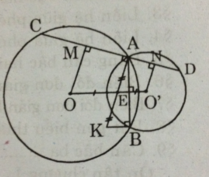 Kẻ OM ⊥ AD.
Kẻ OM ⊥ AD.
Theo tính chất đường kính vuông góc với một dây, ta có: MA = MC
Tương tự, kẻ O'N ⊥ AD => NA = ND.
Ta có:
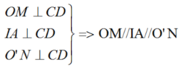
Vậy tứ giác OMNO' là hình thang vuông.
Ta còn có: IO = IO' (gt) và IA // OM
Do đó IA là đường trung bình của hình thang OMNO'.
=> AM = AN hay 2AM = 2AN
Hay AC = CD (đpcm)

a: Xét tứ giác ODAE có
góc ODA+góc OEA=180 độ
=>ODAE là tứ giác nội tiếp
b: \(AE=\sqrt{\left(3R\right)^2-R^2}=2\sqrt{2}\cdot R\)
\(OI=\dfrac{OE^2}{OA}=\dfrac{R^2}{3R}=\dfrac{R}{3}\)
c: Xét ΔDIK vuông tại I và ΔDHE vuông tại H có
góc IDK chung
=>ΔDIK đồng dạng vơi ΔDHE
=>DI/DH=DK/DE
=>DH*DK=DI*DE=2*IE^2

@Thiện Nhân@Thiên Thảo@Guyo@Nguyễn Văn Toàn@Sky SơnTùng
b: Gọi H là giao của AB và OO'
=>OO' vuông góc với AB tại H và H là trung điểm của AB
Xét ΔABK có AH/AB=AM/AK
nên HM//BK
=>BK vuông góc với AB
c: Xét (O) có
ΔABE nội tiếp
AE là đường kính
Do đó: ΔABE vuông tại B
Xét (O') có
ΔAKF nội tiếp
AF là đương kính
Do đó: ΔAKF vuông tại K
Xét (O') có
ΔABF nội tiếp
AF là đường kính
Do đó: ΔABF vuông tại B
góc ABK+góc ABE=90+90=180 độ
=>K,B,E thẳng hàng(1)
góc ABF+góc ABE=90+90=180 độ
nên B,F,E thẳng hàng(2)
Từ (1), (2) suy ra E,B,K,F thẳng hàng
=>OO'//EF
d: Xét ΔAKF có MO'//FK
nên MO'/FK=AO'/AF=1/2
Xét ΔAEK có OM//EK
nên OM/EK=AO/AE=1/2
=>OM/EK=O'M/FK
=>EK=KF
=>K là trung điểm của EF
=>

b: Gọi giao của AB và OO' là M
=>M là trung điểm của AB và OO' vuông góc với AB tại M
Xét ΔABK có AM/AB=AI/AK
nên MI//BK
=>BK vuông góc với AB
c:
Xét (O) có
ΔABE nội tiếp
AE là đường kính
DO đó: ΔABE vuông tại B
Xet (O') có
ΔABF nội tiếp
AF là đường kính
Do đó; ΔABF vuông tại B
=>BF vuông góc với AB
góc EBF=góc EBA+góc FBA=90+90=180 độ
=>E,B,F thẳng hàng(1)
góc ABE+góc ABK=90+90=180 độ
nên E,B,K thẳng hàng(2)
Từ (1), (2) suy ra E,B,K,F thẳng hàng