
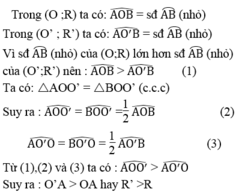
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


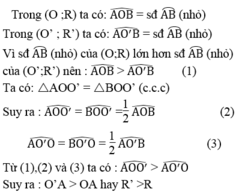

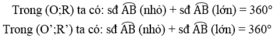
Vì số đo cung lớn AB của (O;R) nhỏ hơn số đo cung lớn AB của (O’;R’) nên số đo cung nhỏ AB của (O;R) lớn hơn số đo cung nhỏ AB của (O’;R’)
Như vậy, trường hợp này tương tự như giả thiết trong câu a.Chứng minh tương tự ta được R’ > R

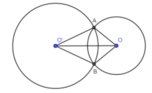
Vì số đo hai cung nhỏ của (O;R) và (O’;R’) bằng nhau nên góc ở tâm của chúng bằng nhau
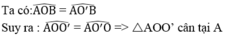
Suy ra : OA = O’A hay R = R’


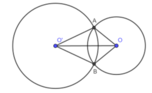
`a,` Ta có: `AO=OB(=R)`
Và: `AB=R` (giả thiết).
`=>AO=AB=BO`
Xét \(\Delta ABO\) có:
`AO=OB=AB(cmt)`
`=>` \(\Delta ABO\) là tam giác đều.
`b,` Ta có: \(\Delta ABO\) là tam giác đều nên:
`=>` \(\widehat{AOB}=60^0\)
Lại có: \(\widehat{AOB}=\dfrac{1}{2}sđ\stackrel\frown{AnB}\) (góc nội tiếp).
\(\Rightarrow sđ\stackrel\frown{AnB}=2\widehat{AOB}=2\cdot60^0=120^0\)
\(\Rightarrow sđ\stackrel\frown{AmB}=360^0-sđ\stackrel\frown{AnB}=360^0-120^0=240^0\)
`c,` Ta có: \(\widehat{AOB}+\widehat{BOC}=180^0\) (kề bù).
\(\Rightarrow\widehat{BOC}=180^0-\widehat{AOB}=180^0-60^0=120^0\)
Mặt khác: \(sđ\stackrel\frown{BnC}=\widehat{BOC}=120^0\) (góc ở tâm).
\(\Rightarrow sđ\stackrel\frown{CAB}=360^0-sđ\stackrel\frown{BnC}=360^0-120^0=240^0\)

a) Xét ΔOAB có OA=OB=AB(=R)
nên ΔOAB đều(Dấu hiệu nhận biết tam giác đều)
\(\Leftrightarrow\widehat{AOB}=60^0\)
hay \(sđ\stackrel\frown{AB}=60^0\)