Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: `\hat(tOz)` và `\hat(t'Oz')` là 2 góc đối đỉnh.
`=> \hat(tOz) = \hat(t'Oz)`
Mà `\hat(tOz) + \hat(t'Oz) = 110^o`
`<=> \hat(tOz) = \hat(t'Oz) = 110^o : 2 =55^o`
`=> \hat(t'Oz)=\hat(tOz') = 180^o - 55^o=125^o`
vì \(\angle\left(tOz\right)=\angle\left(t'Oz'\right)\)(đối đỉnh)
\(=>\angle\left(tOz\right)+\angle\left(t'Oz'\right)=110< =>\angle\left(tOz\right)=\angle\left(t'Oz'\right)=\dfrac{110}{2}=55^o\)
\(=>\angle\left(tOz'\right)=\angle\left(t'Oz\right)=180-55=125^o\)

1,
Ta có : xOz + zOy = 180 độ( kề bù)
hay: xOz +47độ= 180 độ
xOz = 180 độ - 47 độ = 133độ.
2)
- Hai góc vuông không đối đỉnh là : góc xAy và góc x'Ax.
3)
4)
- các góc bằng nhau là :O1=O4 ; O2 = O5 ; O3 = z'Ox' ( đối đỉnh)
( viết số vào chân bên phải của góc và viết đúng kí hiệu góc , độ nka)

a) Ta có: ABDˆ=900,ABD^=900 và ACDˆ=900ACD^=900
⇔ABDˆ=ACDˆ⇔ABD^=ACD^
⇒ABCˆ+CBDˆ=ACBˆ+BCDˆ⇒ABC^+CBD^=ACB^+BCD^
Mà ABCˆ=ACBˆABC^=ACB^ (Tam giác ABC cân tại A)
⇔CBDˆ=BCDˆ⇔CBD^=BCD^
⇔ΔBCD⇔ΔBCD cân tại D
b) Xét tam giác ABD và tam giác ACD, có:
AB=ACAB=AC (Tam giác ABC cân tại A)
BD=CD (Tam giác BCD cân tại D)
ABDˆ=ACDˆ=900
⇔ΔABD=ΔACD (Hai cạnh góc vuông)
⇔BADˆ=CADˆ(Hai cạnh tương ứng)
=> AD là tia phân giác góc A
Lại có: ADBˆ=ADCˆ (ΔABD=ΔACD)
=> DA là tia phân giác góc D
Học tốt
https://h.vn/hoi-dap/tim-kiem?q=Cho+tam+gi%C3%A1c+ABC+c%C3%A2n+t%E1%BA%A1i+A.+Qua+B+k%E1%BA%BB+%C4%91%C6%B0%E1%BB%9Dng+th%E1%BA%B3ng+vu%C3%B4ng+g%C3%B3c+v%E1%BB%9Bi+AB,+qua+C+k%E1%BA%BB+%C4%91%C6%B0%E1%BB%9Dng+th%E1%BA%B3ng+vu%C3%B4ng+g%C3%B3c+v%E1%BB%9Bi+AC,+ch%C3%BAng+c%E1%BA%AFt+nhau+%E1%BB%9F+D.+Ch%E1%BB%A9ng+minh:++a.+Tam+gi%C3%A1c+BDC+c%C3%A2n.+++b.+AB+l%C3%A0+tia+ph%C3%A2n+gi%C3%A1c+c%E1%BB%A7a+g%C3%B3c+A+++++++DA+l%C3%A0+ph%C3%A2n+gi%C3%A1c+c%E1%BB%A7a+g%C3%B3c+D++c.+AD+vu%C3%B4ng+g%C3%B3c+v%E1%BB%9Bi+BC+v%C3%A0+AD+%C4%91i+qua+trung+%C4%91i%E1%BB%83m+c%E1%BB%A7a+BC.&id=558420
bạn tham khảo nhé

\(a)\)
\(zz'\) và \(tt'\)cắt nhau tại \(O\)và có một góc vuông
=> Các góc còn lại đều vuông
\(\Rightarrow\widehat{tOz}=\widehat{zOt'}=\widehat{t'Oz'}=\widehat{tOz'}=90^o\)
\(b)\)
Có hai cặp góc nhọn đối đỉnh:
\(+)\)\(\widehat{xOt};\widehat{x'Ot'}\)
\(+)\)\(\widehat{xOz};\widehat{x'Oz'}\)
Có hai cặp góc tù đối đỉnh:
\(+)\)\(\widehat{xOt'};\widehat{x'Ot}\)
\(+)\)\(\widehat{x'Oz};\widehat{xOz'}\)

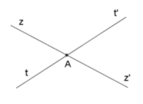
Vì hai đường thẳng zz' và tt' cắt nhau tại A nên Az' là tia đối của tia Az, At' là tia đối của tia At. Vậy góc đối đỉnh với z A t ' ⏜ l à z ' A t ⏜ .
Chọn đáp án B.

a) Vì zz' cắt tt' tại A
=> tAz = z'At' = 60° ( đối đỉnh)
Mà tAz + tAz' = 180° ( kề bù)
=> tAz' = 180° - 60° = 120°
=> tAz' = zAt' = 120° ( đối đỉnh)
b) Vì Am là phân giác tAz
=> tAM = zAM = \(\frac{60°}{2}=30°\)
Vì An là phân giác z'At'
=> z'AN = t'AN = \(\frac{60°}{2}=30°\)
Mà MAN = MAt + tAz' + z'AN
=> MAN = 30° + 30° + 120°
=> MAN = 180°
=> MAN là góc bẹt
=> AM là tia đối của AN