Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Cho hai điện trở R1 và R2. Hãy chứng minh rằng:
a. Khi cho dòng điện chạy qua đoạn mạch gồm R1 và R2 mắc nối tiếp thì nhiệt lượng tỏa ra ở mỗi điện trở này tỉ lệ thuận với các điện trở đó: #Hỏi cộng đồng OLM #Vật lý lớp 9
a) Rtd= \(\frac{1}{R_1}+\frac{1}{R_2}\)= \(\frac{1}{15}+\frac{1}{10}\)=6 \(\Omega\)
b) I=\(\frac{U}{R}\)(định luật ôm)=\(\frac{18}{6}\)=3(A)
Vì R 1 và R 2 mắc nối tiếp nên chúng có cùng cường độ dòng điện chạy qua. Gọi nhiệt lượng tỏa ra ở các điện trở này tương ứng là Q 1 và Q 2 .
Ta có: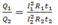 
vì
I
1
=
I
2
(
R
1
nối tiếp với
R
2
) và
t
1
=
t
2
suy ra 
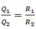
ta có:
U2=I2R2=34.2V
do U1=U2=U3=U nên U=34.2V
ta lại có:
\(I_1=\frac{U_1}{R_1}=1.425A\)
\(I_3=\frac{U_3}{R_3}=0.95A\)
mà I=I1+I2+I3=1.425+0.95+1.9=4.275A
Đối với đoạn mạch gồm hai điện trở mắc song song, hiệu điện thế giữa hai đầu điện trở R1 bằng hiệu điện thế giữa hai đầu R2, tức là U1 = U2. Từ đó ta có I1R1 = I2R2, suy ra \(\dfrac{I_1}{I_2}=\dfrac{R_1}{R_2}\)
Đáng ra phải là chọn câu đúng chứ:
A. Điện trở tương đương R của n điện trở r mắc nối tiếp : R=n.r
B.điện trở tương đương R của n điện trở r mắc song song : R=rnrn
C.Điện trở tương đương của mạch mắc song song nhỏ hơn điện trở mỗi thành phần
D.Trong đoạn mạch mắc song song cường độ dòng điện chạy qua các điện trở là bằng nhau
có R//R(ban đầu)
\(=>U=2.Rtd=2.\dfrac{R}{2}=R\left(V\right)\)
R//R//R'
\(=>\dfrac{1}{Rtd}=\dfrac{1}{R}+\dfrac{1}{R}+\dfrac{1}{2R}=>RTd=\dfrac{2}{5}R\)
\(=>I=\dfrac{U}{Rtd}=\dfrac{R}{\dfrac{2}{5}R}=\dfrac{5}{2}A=>Ir'=0,5A\)
Theo định luật Ôm : \(I=\dfrac{U}{R}\Rightarrow U=I.R\)
nên \(U_1=I_1R_1\)
\(U_2=I_2R_2\)
\(\Rightarrow\) \(\dfrac{U_1}{U_2}=\dfrac{I_1R_1}{I_1R_2}\)
mà \(R_1\) nt \(R_2\) nên \(I_1=I_2\) :
\(\Rightarrow\) \(\dfrac{U_1}{U_2}=\dfrac{R_1}{R_2}\left(đpcm\right)\)
Trong mạch mắc nối tiếp, cường độ dòng điện chạy qua R1 và R2 là như nhau, ta có
I = , từ đó suy ra
Vì R 1 và R 2 mắc song song với nhau nên hiệu điện thế U giữa hai đầu của chúng là như nhau.
Ta có: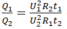
vì
U
1
=
U
2
(
R
1
song song với
R
2
)và
t
1
=
t
2
Suy ra