Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi R1,R2 lần lượt là x,y(ôm)
->hệ pt: \(\left\{{}\begin{matrix}x+y=100\\\dfrac{xy}{x+y}=16\end{matrix}\right.< =>\left\{{}\begin{matrix}y=100-x\left(1\right)\\\dfrac{x\left(100-x\right)}{x+100-x}=16\left(2\right)\end{matrix}\right.\)
giải pt(2)
\(=>\dfrac{100x-x^2}{100}=16< =>-x^2+100x-1600=0\)
\(\Delta=100^2-4\left(-1600\right)\left(-1\right)=3600>0\)
\(=>\left[{}\begin{matrix}x1=\dfrac{-100+60}{-2}=20\\x2=\dfrac{-100-60}{-2}=80\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}y1=80\\y2=20\end{matrix}\right.\)
vậy (R1;R2)={(20;80),(80;20)}

Gọi R = R2
Khi mắc song song R t đ 1 = R 1 . R 2 R 1 + R 2 = 2 R 3
Công của dòng điện: A 1 = U . I . t = U 2 R t đ 1 . t = 3 U 2 2 R . t
Khi mắc nối tiếp: R t đ 2 = R 1 + R 2 = 3 R .
Công của dòng điện: A 2 = U 2 R t đ 2 . t = U 2 3 R . t
Ta có: ⇒ A 1 A 2 = 9 2 = 4 , 5 ⇒ A 1 = 4 , 5 A 2
→ Đáp án B

Khi mắc nối tiếp thì điện trở tương đương là 9Ω nên ta có:
\(R_{\text{tđ}}=R_1+R_2=9\Omega\) (1)
\(\Rightarrow R_2=9-R_1\left(2\right)\)
Khi mắt nối tiếp thì điện trở tương đương là 2Ω nên ta có:
\(R_{\text{tđ}}=\dfrac{R_1R_2}{R_1+R_2}=2\Omega\)
\(\Rightarrow R_1+R_2=\dfrac{R_1R_2}{2}\) (3)
Thay (3) vào (1) ta có:
\(\Rightarrow9=\dfrac{R_1R_2}{2}\Rightarrow R_1R_2=18\) (44)
Thay (3) vào (4) ta có:
\(R_1\cdot\left(9-R_1\right)=18\)
\(\Rightarrow9R_1-R^2_1=18\)
\(\Rightarrow R^2_1-9R_1+18=0\)
\(\Rightarrow\left[{}\begin{matrix}R_1=3\Omega\\R_1=6\Omega\end{matrix}\right.\)
TH1: \(R_1=3\Omega\)
\(\Rightarrow R_2=9-3=6\Omega\)
TH2: \(R_2=6\Omega\)
\(\Rightarrow R_2=9-6=3\Omega\)

Vì Rtđ >R1(16>10)
nên MCD R1nt R2
Điện trở R2 là
\(R_2=R_{tđ}-R_1=16-10=6\left(\Omega\right)\)
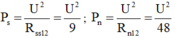
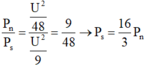
Theo đề bài ta có
`R_(tđ) = (R_1 *R_2)/(R_1 +R_2)`
mà ` (R_1 +R_2)/4 = R_(tđ)`
`=> (R_1 +R_2)/4 = (R_1 *R_2)/(R_1+ R_2)`
`=>R_1=R_2 ` ( bạn làm ra nháp sẽ ra kết quả)
Vậy `R_1 = R_2`
gọi R1 là x , R2 là y
có \(\dfrac{4.x.y}{x+y}\)=x+y <=> 4xy = x^2 + 2xy + y^2 <=> X^2 - 2xy +y^2 = 0
<=> -x(y-x) + y(y-x) = 0 <=> (y-x)^2 = 0 => y = x
vậy r1 = r2