Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

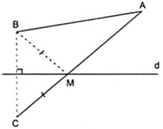
Vẽ điểm C đối xứng với B qua đường thẳng d, giả sử tìm được điểm M trên d thì MB = MC ( 1 ).
Do A, B, d cố định nên C cũng cố định suy ra độ dài đoạn AC không đổi.
Áp dụng bất đẳng thức tam giác ta có vào Δ AMC ta được: MA + MC ≥ AC ( 2 )
Dấu bằng xảy ra khi M nằm giữa A và C hay M là giao điểm của AC và đường thẳng d
Từ ( 1 ) và ( 2 ) suy ra MA + MB nhỏ nhất bằng AC khi M là giao điểm của AC và đường thẳng d

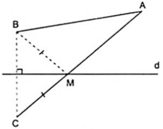
Vẽ điểm C đối xứng với B qua đường thẳng d, giả sử tìm được điểm M trên d thì MB = MC ( 1 ).
Do A, B, d cố định nên C cũng cố định suy ra độ dài đoạn AC không đổi.
Áp dụng bất đẳng thức tam giác ta có vào Δ AMC ta được: MA + MC ≥ AC ( 2 )
Dấu bằng xảy ra khi M nằm giữa A và C hay M là giao điểm của AC và đường thẳng d
Từ ( 1 ) và ( 2 ) suy ra MA + MB nhỏ nhất bằng AC khi M là giao điểm của AC và đường thẳng d

Từ A kẽ AH vuông góc d và A'H đối xứng với AH
R là giao điểm A'B và d.
Vì AH=A'H (cách dựng) và HP vuông góc với AA' nên dễ dàng suy ra tam giác APA' cân => AP=A'P
Áp dụng t/chất đường gấp khúc ta có:
AP+PB=A'P+PB>=A'B
Dấu ''='' xảy ra khi 3 điểm A',P,B thẳng hàng hay P trùng R

C đối xứng với A qua d => d là trung trực của AC
D; E thuộc d => EA = EC và DA = DC
ta có : AD + DB = DC + DB = CB
AE + EB = EC + EB
Trong tam giác BEC có: BC < EC + EB => AD + BD < AE + BE
b﴿ Giả sử bạn Tú đến điểm E bất kì trên d
ta có: Quãng đường bạn cần đi là AE + EB
mà AE + EB = CE + EB
ta luôn có: CE + EB ≥ CB
đê đi gần nhất thì CE + EB nhỏ nhất = CB
Dấu "=" xảy ra khi E trùng với D
vậy....

Cách giải:
- Tìm điểm A’ đối xứng với A qua d
- Nối A’B cắt d tại M . M chính là điểm cần tìm .
- Thật vậy : Vì A’ đối xứng với A qua d cho nên \(MA=MA'\left(1\right)\). Do đó: \(MA+MB=MA'+MB=A'B.\) .
- Giả sử tồn tại M’ khác M thuộc d thì : \(M'A+M'B=M'A'+M'B\ge A'B\). Dấu bằng chỉ xảy ra khi \(A'M'B'\) thẳng hàng . Nghĩa là M trùng với M’.
Chúc bạn học tốt!