Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
M + N = (x2 – 2yz + z2) + (3yz – z2 + 5x2)
= x2 – 2yz + z2 + 3yz – z2 + 5x2
= (x2 + 5x2) + (z2 – z2) + (-2yz + 3yz)
= 6x2 + yz
M + N = x2 - 2yz + z2 + 3yz - z2 + 5x2
= 6x2 + yz.
Chúc bạn học tốt@@
Cách 1:
M - N = (0,5x4 – 4x3 + 2x – 2,5) - ( 2x3 + x2 + 1,5)
= 0,5x4 – 4x3 + 2x – 2,5 - 2x3 - x2 - 1,5
= 0,5x4 + (– 4x3 - 2x3 ) - x2 + 2x + (-2,5 - 1,5)
= 0,5x4 + (– 6x3 ) - x2 + 2x + (-4)
= 0,5x4 – 6x3 - x2 + 2x – 4
Cách 2:
tìm đa thức A biết :
a) A + (x2 + y2 ) = 5x2 + 3y2 - xy
A = 5x2 + 3y2 - xy - (x2 + y2 )
A = 5x2 + 3y2 - xy - x2 - y2
A = ( 5x2 - x2 ) + ( 3y2 - y2 ) - xy
A = 4x2 + 2y2 - xy
Vậy A = 4x2 + 2y2 - xy
b) A - ( xy + x2 - y2 ) = x2+ y2
A = x2+ y2 + xy + x2 - y2
A = ( x2 + x2 ) + ( y2 - y2 ) + xy
A = 2x2 + xy
Vậy A = 2x2 + xy
cho hai đa thức :
a) M+N = x2 - 2yz + z2 + 3yz - z2 + 5x2
M + N = ( x2 + 5x2 ) - ( 2yz - 3yz ) + ( z2 - z2 )
M + N = 6x2 + yz
b) M - N = x2 - 2yz + z2 - ( 3yz - z2 + 5x2 )
M - N = x2 - 2yz + z2 - 3yz + z2 - 5x2
M - N = ( x2 - 5x2 ) - ( 2yz + 3yz ) + ( z2 + z2 )
M - N = -4x2 - 5yz + 2z2
N - M = 3yz - z2 + 5x2 - ( x2 - 2yz + z2 )
N - M = 3yz - z2 + 5x2- x2 + 2yz - z2
N - M = ( 3yz + 2yz ) - ( z2 + z2 ) + ( 5x2 - x2 )
N - M = 5yz - 2z2 + 4x2
a) M+N = x2 - 2yz + z2 + 3yz - z2 + 5x2
M + N = ( x2 + 5x2 ) - ( 2yz - 3yz ) + ( z2 - z2 )
M + N = 6x2 + yz
b) * M - N = x2 - 2yz + z2 - ( 3yz - z2 + 5x2 )
M - N = x2 - 2yz + z2 - 3yz + z2 - 5x2
M - N = ( x2 - 5x2 ) - ( 2yz + 3yz ) + ( z2 + z2 )
M - N = -4x2 - 5yz + 2z2
* N - M = 3yz - z2 + 5x2 - ( x2 - 2yz + z2 )
N - M = 3yz - z2 + 5x2- x2 + 2yz - z2
N - M = ( 3yz + 2yz ) - ( z2 + z2 ) + ( 5x2 - x2 )
N - M = 5yz - 2z2 + 4x2
___Xin lỗi nha phần kia bị lỗi____
\(M+N=\left(2x^2+3xy+2y^2\right)+\left(-5x^2-3xy+2y^2+5\right)\\ =2x^2+3xy+2y^2-5x^2-3xy+2y^2+5\\ =-3x^2+4y^2+5\\ M-N=\left(2x^2+3xy+2y^2\right)-\left(-5x^2-3xy+2y^2+5\right)\\ =2x^2+3xy+2y^2+5x^2+3xy-2y^2-5\\ =7x^2+6xy-5\)
\(N-M=\left(-5x^2-3xy+2y^2+5\right)-\left(2x^2+3xy+2y^2\right)\\ =-5x^2-3xy+2y^2+5-2x^2-3xy-2y^2\\ =-7x^2-6xy+5\)
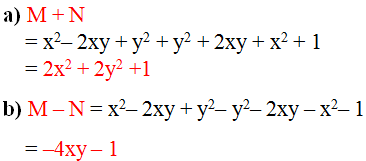
M – N = (x2 – 2yz + z2) – (3yz – z2 + 5x2)
= x2 – 2yz + z2 - 3yz + z2 - 5x2
= (x2 – 5x2) – (2yz + 3yz) + (z2 + z2)
= -4x2 – 5yz + 2z2
N – M = (3yz – z2 + 5x2) – (x2 – 2yz + z2)
= 3yz – z2 + 5x2 - x2 + 2yz - z2
= (3yz + 2yz) – (z2 + z2) + (5x2 – x2)
= 5yz – 2z2 + 4x2.