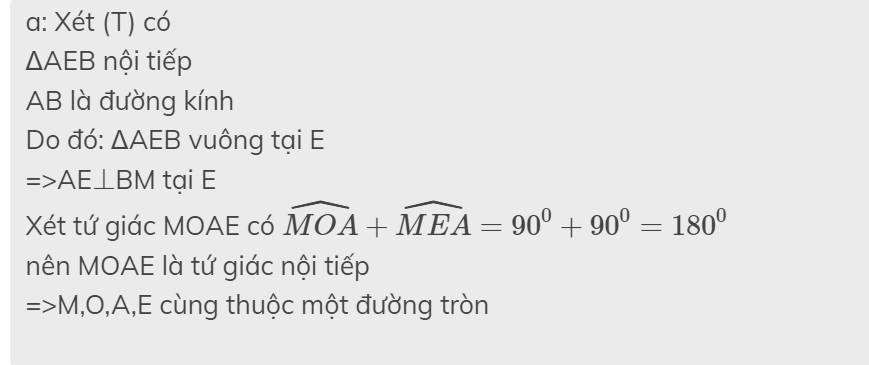Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có \(\Delta HEB~\Delta KFB\left(g-g\right)\)=> \(\frac{HE}{KF}=\frac{BH}{BK}\)=> \(\frac{HE^2}{KF^2}=\frac{BH^2}{BK^2}\)(1)
Có \(HE^2=EA.EO\)(TỰ XÉT TAM GIÁC NHA) (2)
\(KF^2=FA.FO\)(3)
tỪ (1),(2),(3) => \(\frac{EA.EO}{FA.FO}=\frac{BH^2}{BK^2}\)(đpcm)

a: Xét (T) có
ΔAEB nội tiếp
AB là đường kính
Do đó: ΔAEB vuông tại E
=>AE\(\perp\)BM tại E
Xét tứ giác MOAE có \(\widehat{MOA}+\widehat{MEA}=90^0+90^0=180^0\)
nên MOAE là tứ giác nội tiếp
=>M,O,A,E cùng thuộc một đường tròn


a, Chỉ ra |OI – OK| < IK < OI + OK => (1) và (k) luôn cắt nhau
b, Do OI=NK, OK=IM => OM=ON
Mặt khác OMCN là hình chữ nhật => OMCN là hình vuông
c, Gọi{L} = KB ∩ MC, {P} = IBNC => OKBI là Hình chữ nhật và BNMI là hình vuông
=> ∆BLC = ∆KOI
=> L B C ^ = O K I ^ = B I K ^
mà B I K ^ + I B A ^ = 90 0
L B C ^ + L B I ^ + I B A ^ = 180 0
d, Có OMCN là hình vuông cạnh a cố định
=> C cố định và AB luôn đi qua điểm C