Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tg ABEC có CE // AB ( gt )
=> Tg ABEC là hình thang
+) ΔOAB có OA = OB ( gt )
=> ΔOAB cân ở O
=> \(\widehat{A_1}=\widehat{B_1}\)
+) Hình thang ABEC có \(\widehat{A_1}=\widehat{B_1}\)
=> Hình thang ABEC là hình thang cân ( DHNB hình thang cân )

Câu 2:
a: Ta có: A và B đối xứng nhau qua Ox
nên Ox là đường trung trực của AB
=>OA=OB
mà Ox là đường cao
nên Ox là tia phân giác của góc AOB(1)
Ta có: A và C đối xứng nhau qua Oy
nen OA=OC
=>ΔOAC cân tại O
mà Oy là đường cao
nên OY là phân giác của góc AOC(2)
Ta có: OA=OB
OA=OC
Do đó: OB=OC
b: Từ (1) và (2) suy ra \(\widehat{BOC}=\widehat{BOA}+\widehat{COA}=2\cdot\widehat{xOy}=140^0\)

a) Xét ΔOAB và ΔOCD có
\(\dfrac{OA}{OC}=\dfrac{OB}{OD}\left(=\dfrac{3}{2}\right)\)
\(\widehat{AOB}\) chung
Do đó: ΔOAB\(\sim\)ΔOCD(c-g-c)

a: Xét ΔOAH và ΔOBH có
AO=BO
OH chung
AH=BH
=>ΔOHA=ΔOHB
b: ΔOHA=ΔOHB
=>góc OHA=góc OHB=180/2=90 độ
=>OH vuông góc AB
c: Xét ΔOAC và ΔOBC có
OA=OB
góc AOC=góc BOC
OC chung
=>ΔOAC=ΔOBC
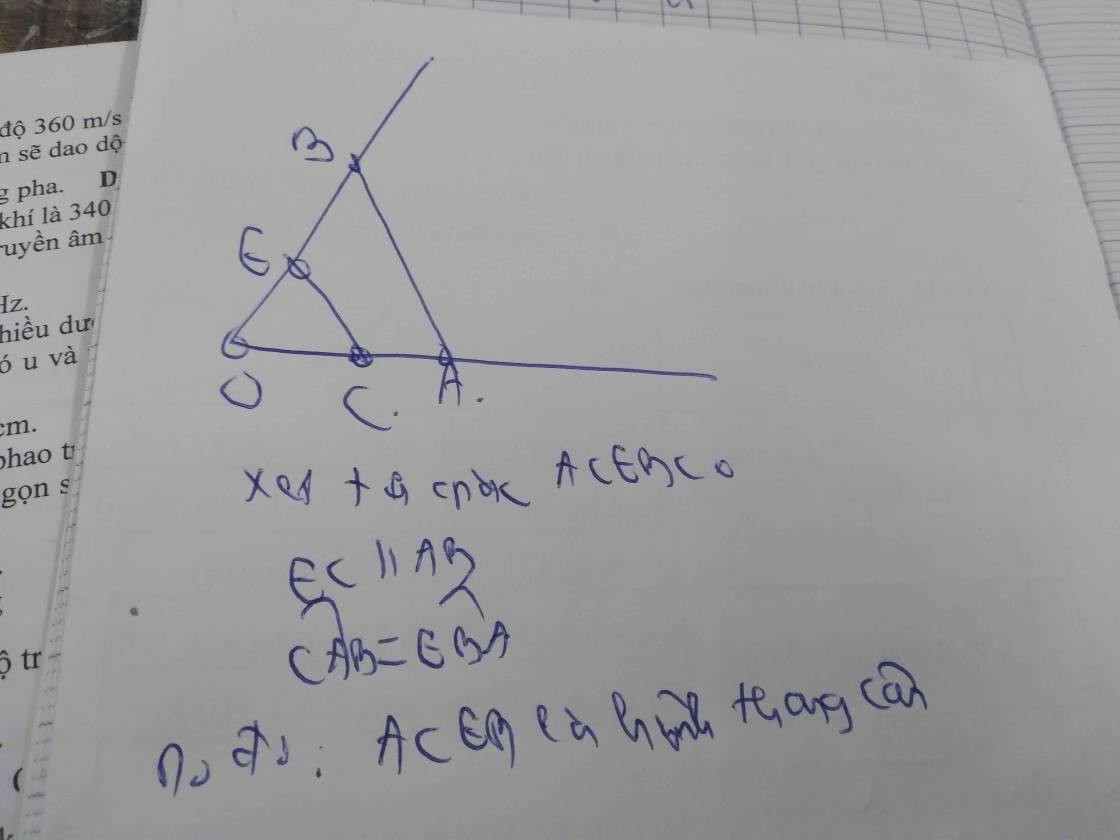
Xét tứgiác ACEB có
EC//AB
góc CAB=góc EBA
Do đó: ACEB là hình thang cân