Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

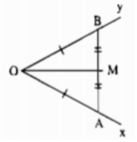
- Dùng thước chia khoảng, trên Ox lấy điểm A, trên Oy lấy điểm B sao cho OA = OB.
- Nối AB.
- Dùng thước chia khoảng để đo đoạn AB, lấy trung điểm M của AB.
- Kẻ tia OM.
Khi đó, OM là tia phân giác của góc ∠xOy.
Chứng minh
Tam giác ABO có OA = OB ( cách dựng) nên tam giác OAB cân tại O.
Lại có: OM là đường trung tuyến nên OM cũng là đường phân giác của ∠(AOB). ( tính chất tam giác cân)
Vậy OM là tia phân giác của ∠(xOy).

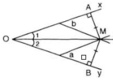
(Từ bài tập 12 ta biết rằng: độ dài đường vuông góc giữa hai đường thẳng song song chính là khoảng cách giữa hai đường thẳng đó.)
Gọi A, B lần lượt là chân đường cao hạ từ M xuống Ox, Oy ⇒ MA, MB lần lượt là khoảng cách từ M đến Ox, Oy.
Theo cách vẽ bằng thước hai lề và từ bài tập 12 ta suy ra: MA = MB (cùng bằng khoảng cách hai lề của thước) hay điểm M cách đều hai cạnh của góc xOy.
Áp dụng định lý 2 suy ra: OM là tia phân giác của góc xOy.

Hướng dẫn :
Theo cách vẽ thì M cách đều hai cạnh Ox, Oy (cùng bằng khoảng cách 2 lề của chiếc thước
Vì M cách đều Ox, Oy nên theo định lí đảo M thuộc phân giác của ˆxOyxOy^ hay OM là phân giác của ˆ

Hướng dẫn :
Theo cách vẽ thì M cách đều hai cạnh Ox, Oy (cùng bằng khoảng cách 2 lề của chiếc thước
Vì M cách đều Ox, Oy nên theo định lí đảo M thuộc phân giác của ˆxOyxOy^ hay OM là phân giác của ˆ
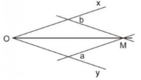
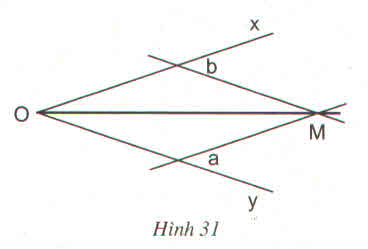
1.Vẽ đường thẳng a song song với Ox
2.Vẽ đường thẳng b song song với Oy
3.Gọi giao điểm của a và b là M
4. Nối O với M. Đó chính là đường phân giác của góc xOy