Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kẻ đường cao BH
diện tích tam giác ABC là \(\frac{1}{2}BH.AC=\frac{1}{2}ABsin\widehat{A}.\left(6-AB\right)\le\frac{9}{2}sin\widehat{A}\) vì AB(6-AB)= 6AB-AB2 = 9- (AB-3)2 \(\le9\)
vậy diện tích ABC lớn nhất khi AB-3=0 hay AB=AC =3

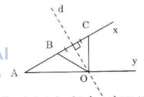
- Tâm O là giao điểm giữa đường trung trực của BC và tia Ay. Nên ta có cách dựng:
+ Dựng đường trung trực (d) của BC. (d) cắt tia Ay tại O.
+ Vẽ đường tròn (O, OB). Đường tròn này đi qua B, C. Đó là đường tròn cần dựng.
- Chứng minh:
+ Vì O ∈ đường trung trực (d) của BC nên OB = OC. Suy ra (O, OB) đi qua B, C
+ Vì O ∈ Ay nên (O, OB) thỏa mãn điều kiện đề bài.
QUẢNG CÁO
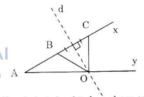
- Tâm O là giao điểm giữa đường trung trực của BC và tia Ay. Nên ta có cách dựng:
+ Dựng đường trung trực (d) của BC. (d) cắt tia Ay tại O.
+ Vẽ đường tròn (O, OB). Đường tròn này đi qua B, C. Đó là đường tròn cần dựng.
- Chứng minh:
+ Vì O ∈ đường trung trực (d) của BC nên OB = OC. Suy ra (O, OB) đi qua B, C
+ Vì O ∈ Ay nên (O, OB) thỏa mãn điều kiện đề bài.


Đặt AC = x; BD = y (x, y > 0)
Ta có \(\Delta ACM\sim\Delta BMD\left(g-g\right)\Rightarrow\frac{AC}{MB}=\frac{AM}{BD}\)
\(\Rightarrow AC.BD=AM.MB=const\Rightarrow xy=c=const\)
\(S_{MCD}=S_{ACDB}-S_{ACM}-S_{MBD}=\frac{\left(x+y\right)\left(AM+MB\right)}{2}-\frac{x.AM}{2}-\frac{y.MB}{2}\)
\(=\frac{x.MB+y.AM}{2}\ge\sqrt{xy.MB.AM}=\sqrt{c^2}=c\)
Dấu bằng xảy ra khi x.MB = y.AM, lại có \(xy=MB.AM\Rightarrow\hept{\begin{cases}x=AM\\y=MB\end{cases}}\)
Vậy giá trị nhỏ nhất của \(S_{CMD}=c\left(đvdt\right)\) xảy ra khi AC = AM; BD = BM.

Em tham khảo tại link dưới đây nhé.
Câu hỏi của Linhllinh - Toán lớp 9 - Học toán với OnlineMath

Phân tích
Giải sử đã dựng được đường tròn (O) thỏa mãn đề bài. Tâm O phải thỏa mãn hai điều kiện:
- O nằm trên đường trung trực m của BC.
- O nằm trên tia Ay.
Cách dựng:
- Dựng đường trung trực m của BC, cắt Ay tại O.
- Dựng đường tròn (O;OB), đó là đường tròn phải dựng.
Chứng minh
Vì điểm O THUOC m nên OB=OC, suy ra đường tròn (O; OB) đi qua B và C.
Mặt khácO thuoc Ay , nên đường tròn (O) thỏa mãn đề bài.
Biện luận
Vì m luôn cắt tia Ay tại một điểm O duy nhất nên bài toán luôn có một nghiệm hình.
Phân tích
Giải sử đã dựng được đường tròn (O) thỏa mãn đề bài. Tâm O phải thỏa mãn hai điều kiện:
- O nằm trên đường trung trực m của BC.
- O nằm trên tia Ay.
Cách dựng:
- Dựng đường trung trực m của BC, cắt Ay tại O.
- Dựng đường tròn (O;OB), đó là đường tròn phải dựng.
Chứng minh
Vì điểm O THUOC m nên OB=OC, suy ra đường tròn (O; OB) đi qua B và C.
Mặt khácO thuoc Ay , nên đường tròn (O) thỏa mãn đề bài.
Biện luận
Vì m luôn cắt tia Ay tại một điểm O duy nhất nên bài toán luôn có một nghiệm hình.
ai tích mình tích lại nha