Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bài làm
a, gọi H là tiếp điểm của tiếp tuyến MN
theo giả thuyết 2 tiếp tuyến AM và MH cắt nhau tại M
⇒ AM=MH ( tính chất 2 tiếp tuyến cắt nhau)
theo giả thuyết 2 tiếp tuyến HN cắt BN tại N
⇒ HN=BN ( tính chất 2 tiếp tuyến cắt nhau)
nên ta có: MN=HM=HN=\(\dfrac{1}{2}\)(AOH =HON)=90 độ
vậy góc MON=90 đọ và là tâm giác vuông tại O đường cao OH
b,theo giả thuyết 2 tiếp tuyến AM và MH cắt nhau tại M
⇒ AM=MH ( tính chất 2 tiếp tuyến cắt nhau)
theo giả thuyết 2 tiếp tuyến HN cắt BN tại N
⇒ HN=BN ( tính chất 2 tiếp tuyến cắt nhau)
Theo hệ thức lượng trong tam giác vuông: OI^2=MI.INOH2=MH.HNAM.BN=MI.NI=OI^
Vì vậy AM.BN=MI.NI=OI^2=R^2AM.BN=MH.NH=
\(OH^2\)=\(R^2\)

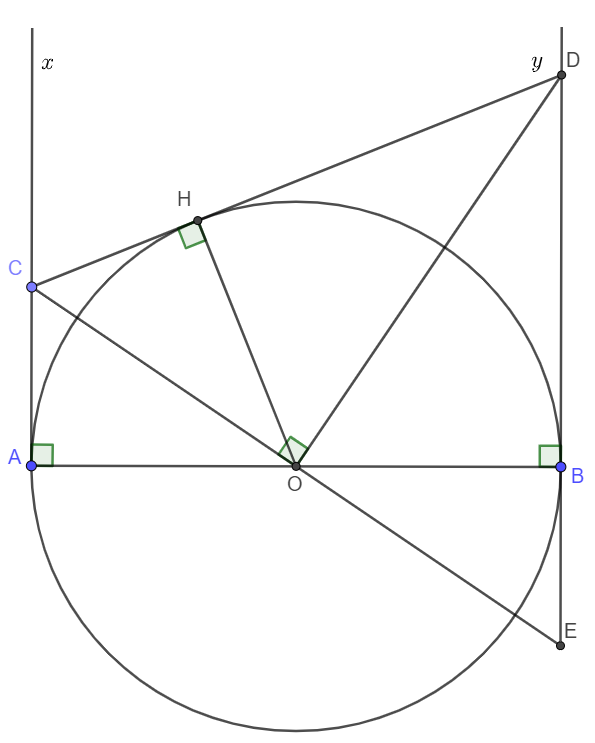
Vẽ OH\perp CD\left(H\in CD\right)OH⊥CD(H∈CD). Ta chứng minh OH = r = OB. (r là bán kính của đường tròn (O) ).
Tia CO cắt tia đối của tia By tại E.
Ta có \Delta OAC=\Delta OBE\left(g.c.g\right)\Rightarrow OC=OEΔOAC=ΔOBE(g.c.g)⇒OC=OE.
Tam giác DEC có DO vừa là đường cao vừa là đường trung tuyến nên DEC là tam giác cân tại D.
Khi đó DO cũng là đường phân giác.
OH\perp DC,OB\perp DE\Rightarrow OH=OB.OH⊥DC,OB⊥DE⇒OH=OB..
Suy ra CD tiếp xúc với (O) tại H.
Ta có OH\perp CD,OH=OB=rOH⊥CD,OH=OB=r.
Vậy CD là tiếp tuyến của đường tròn (O).
Vẽ OH⊥CD(H∈CD). Ta chứng minh OH = r = OB. (r là bán kính của đường tròn (O) ).
Tia CO cắt tia đối của tia By tại E.
Ta có ΔOAC=ΔOBE(g.c.g)⇒OC=OE.
Tam giác DEC có DO vừa là đường cao vừa là đường trung tuyến nên DEC là tam giác cân tại D.
Khi đó DO cũng là đường phân giác.
OH⊥DC,OB⊥DE⇒OH=OB..
Suy ra CD tiếp xúc với (O) tại H.
Ta có OH⊥CD,OH=OB=r.
Vậy CD là tiếp tuyến của đường tròn (O).

a) Vẽ tia CO cắt tia đối của tia By tại E
Xét tam giác vuông AOC và tam giác vuông BOE có :
AO = OB ( gt )
AOC = BOE ( 2 góc đối đỉnh )
\(\implies\) tam giác vuông AOC = tam giác vuông BOE ( cạnh huyền - góc nhọn )
\(\implies\) AC = BE ( 2 cạnh tương ứng )
Xét tam giác vuông DOC và tam giác vuông DOE có :
OD chung
OC = OE ( tam giác vuông AOC = tam giác vuông BOE )
\(\implies\) tam giác vuông DOC = tam giác vuông DOE ( 2 cạnh góc vuông )
\(\implies\) CD = ED ( 2 cạnh tương ứng )
Mà ED = EB + BD
\(\implies\) ED = AC + BD
\(\implies\) CD = AC + BD
c) Xét tam giác DOE vuông tại O có :
OE2 + OD2 = DE2 ( Theo định lý Py - ta - go )
Xét tam giác BOE vuông tại B có :
OB2 + BE2 = OE2 ( Theo định lý Py - ta - go ) ( * )
Xét tam giác BOD vuông tại B có :
OB2 + BD2 = OD2 ( Theo định lý Py - ta - go ) ( ** )
Cộng ( * ) với ( ** ) vế với vế ta được :
OE2 + OD2 = 2. OB2 + EB2 + DB2
Mà OE2 + OD2 = DE2 ( cmt )
\(\implies\) DE2 = 2. OB2 + EB2 + DB2
= 2. OB2 + EB . ( DE - BD ) + DB . ( DE - BE )
= 2. OB2 + EB . DE - EB . BD + DB . DE - DB . BE
= 2. OB2 + ( EB . DE + DB . DE ) - 2 . BD . BE
= 2. OB2 + DE . ( EB + DB ) - 2 . BD . BE
= 2. OB2 + DE2 - 2 . BD . BE
\(\implies\) 2. OB2 - 2 . BD . BE = 0
\(\implies\) 2. OB2 = 2 . BD . BE
\(\implies\) OB2 = BD . BE
Mà BE = AC ( cmt ) ; OB = AB / 2 ( gt )
\(\implies\) AC . BD = ( AB / 2 )2
\(\implies\) AC . BD = AB2 / 4

Câu cuối là gì nhờ
A A A B B B M M M C C C D D D O O O H H H K K K E E E F F F I I I a/Vì C là giao điểm 2 tiếp tuyến (O) nên ta có AC=MC,^OCM=1/2 ^ACD
Tương tự thì BD=DM, ^ODC=1/2 ^BDC.Từ đó suy ra AC+BD=CM+DM=CD và ^COD=90
b/Từ kết quả ở câu a thì ta chỉ cần chứng minh CM.DM=R2=OM2
Ta dễ dàng chứng minh được đẳng thức trên vì ta có \(\Delta OCM~\Delta DOM\left(g.g\right)\)
c/Ta có OC là đường trung trực của AM nên suy ra AM vuông góc OC tại H,H là trung điểm AM
Lại có BM vuông góc với OD tại K,K là trung điểm BM và ^COD=90(cmt)
Suy ra OHMK là hcn
d/Từ câu c suy ra ngay OC//BM, mà O là trung điểm AB nên OC là đtb của tam giác ABE
Suy ra C là trung điểm AE
e/MF cắt HK thì phải
Ta có tam giác AMF có HI//AF,H là trung điểm AM suy ra I là trung điểm MF
f/Gọi T là trung điểm CD, ta dễ thấy (COD) là (T,TO)
Mà ta có TO vuông góc với AB(tính chất đường tb hình thang)
g/ ghi đề dùm

gọi H là điểm tiếp điểm của MN với nữa đường tròn
ta có : OM là tia phân giác của góc AOH (theo tính chất 2 tiếp tuyến cắt nhau)
ON là tia phân giác của góc BOH (theo tính chất 2 tiếp tuyến cắt nhau)
mà 2 góc MOH và HON kề bù \(\Rightarrow\) MON = 900
b) AM = HM và BN = HN (tính chất 2 tiếp tuyến cắt nhau) (1)
nên MN = HM + HN = AM + BN
vậy MN = AM + BN (đpcm)
c) từ (1) ta có : AM.BN = HM.HN
ta lại có : HM HN = OH2 = R2 (hệ thức lượng)
\(\Rightarrow\) AM.BN = R2 (đpcm)

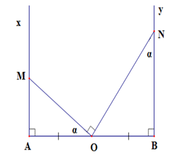
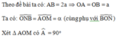
Áp dụng hệ thức về cạnh và góc trong tam giác vuông, ta có:
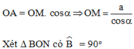
Áp dụng hệ thức về cạnh và góc trong tam giác vuông, ta có:
![]()
Vậy diện tích tam giác MON là:
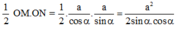
Đáp án cần chọn là: A