Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

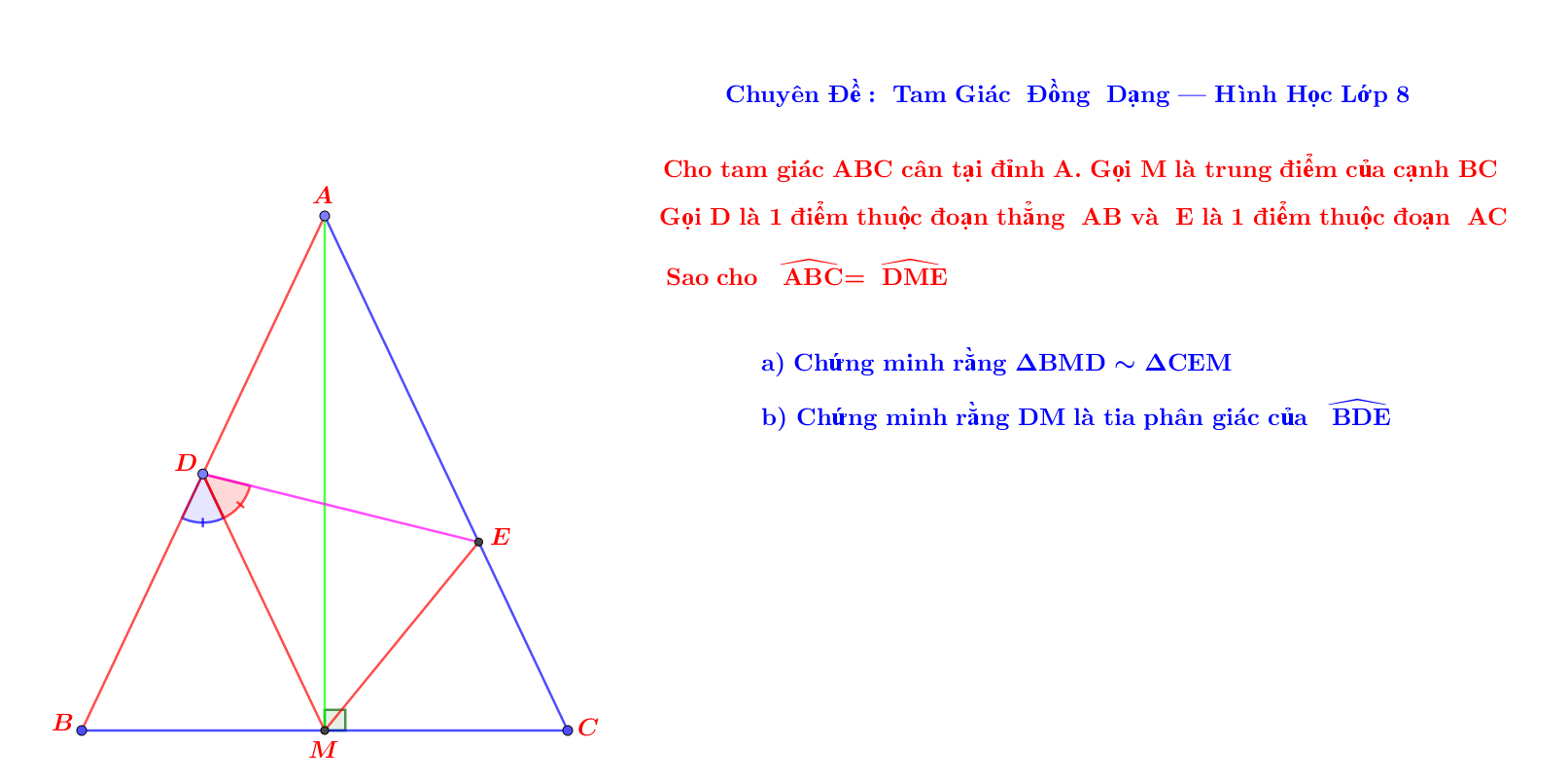
a) \(\widehat{BDM}=180^0-\widehat{BMD}-\widehat{DBM}=180^0-\widehat{BMD}-\widehat{DME}=\widehat{CME}\)
\(\Rightarrow\)△BMD∼△CEM (g-g)
b) \(\Rightarrow\dfrac{BD}{CM}=\dfrac{MD}{EM}\Rightarrow\dfrac{BD}{BM}=\dfrac{MD}{EM}\)
\(\Rightarrow\)△BMD∼△MED (c-g-c).
\(\Rightarrow\widehat{BDM}=\widehat{MDE}\Rightarrow\)DM là tia p/g góc BDE.

bài 3
Gọi giao điểm của EM với AC là K' ( K' \(\in\)AC )
Ta sẽ chứng minh K' \(\equiv\)K
Thật vậy, gọi giao điểm AC và MN là O ; K'N cắt DC tại I
dễ thấy O là trung điểm MN
do MN // EI \(\Rightarrow\frac{MO}{EC}=\frac{K'O}{K'C}=\frac{ON}{CI}\)\(\Rightarrow EC=CI\)
\(\Delta NEI\)có NC là đường cao vừa là trung tuyến nên cân tại N
\(\Rightarrow\)NC là đường phân giác của \(\widehat{ENI}\)
Mà \(\widehat{K'NE}+\widehat{ENI}=180^o\) có \(NM\perp NC\)nên NM là đường phân giác \(\widehat{K'NE}\)( 1 )
mặt khác : NM là đường phân giác \(\widehat{KNE}\) ( 2 )
Từ ( 1 ) và ( 2 ) suy ra \(K'\equiv K\)hay A,K,C thẳng hàng
Trên tia đối tia HC lấy D sao cho HD = HC
Tứ giác DECF có DH = HC ; EH = HF nên là hình bình hành
\(\Rightarrow\)DE // CF
\(\Rightarrow\)DE \(\perp\)CH ; BE \(\perp\)DH
\(\Rightarrow\)E là trực tâm tam giác DBH \(\Rightarrow HE\perp BD\)
Xét \(\Delta DBC\)có DH = HC ; BM = MC nên MH là đường trung bình
\(\Rightarrow\)MH // BD
\(\Rightarrow\)MH \(\perp EF\)

-Bài hình chẳng ai phụ trách giùm mình hết :v (đặc biệt là hình nâng cao).
-Mình cũng xin lỗi vi tối mới làm đc cho bạn nhé.
-Gọi E là giao của AD và BC.
\(\widehat{BAE}=180^0-\widehat{BAD}=\widehat{BCD}\)
\(\Rightarrow\)△ABE∼△CDE (g-g).
\(\Rightarrow\dfrac{AE}{CE}=\dfrac{BE}{DE}\Rightarrow\dfrac{AE}{BE}=\dfrac{CE}{DE}\Rightarrow\)△EAC∼△EBD (c-g-c).
\(\Rightarrow\widehat{ICB}=\widehat{IDA}\Rightarrow\)△IBC∼△IAD (g-g)
\(\Rightarrow\dfrac{IB}{IA}=\dfrac{IC}{ID}\Rightarrow\dfrac{IB}{IC}=\dfrac{IA}{ID}\Rightarrow\)△AIB∼△DIC (c-g-c)
\(\Rightarrow\widehat{IAM}=\widehat{IDN};\dfrac{IA}{ID}=\dfrac{AB}{DC}\Rightarrow\dfrac{IA}{ID}=\dfrac{MA}{ND}\Rightarrow\dfrac{IA}{MA}=\dfrac{ID}{ND}\)
\(\Rightarrow\)△AIM∼△DIN (c-g-c) \(\Rightarrow\widehat{AIM}=\widehat{DIN}\)
Em cám ơn thầy nhiều lắm ạ!
Em đã hiểu bài rồi thầy ạ! Trân trọng sự giúp đỡ của thầy ạ!


a) Xét tam giác ABN và tam giác ACM
có góc A chung, \(\widehat {ABN} = \widehat {ACM}\)
=> ΔABN ∽ ΔACM
b) Có ΔABN ∽ ΔACM
\(\widehat {ANB} = \widehat {AMC}\)
Có \(\widehat {ANB} + \widehat {CNB} = {180^o}\)
\(\widehat {AMC} + \widehat {BMC} = {180^o}\)
=> \(\widehat {CNB} = \widehat {BMC}\)
Xét tam giác IBM và tam giác ICN
Có \(\widehat {CNB} = \widehat {BMC}\) và \(\widehat {IBM} = \widehat {ICN}\)
=> ΔIBM ∽ ΔICN (g.g)
=> \(\frac{{IB}}{{IC}} = \frac{{IM}}{{IN}}\)
=> IB.IN=IC.IM