Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

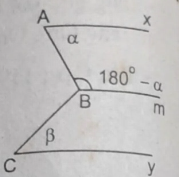
a) Ta có: \(\alpha+\widehat{ABm}=\alpha+180^0-\alpha=180^0\)
Mà 2 góc này là 2 góc trong cùng phía
=> Ax//Bm
b) Trên tia đối Bm kẻ Bn
=> Bn//Ax
\(\Rightarrow\alpha=\widehat{ABn}\)(so le trong)
\(\Rightarrow\widehat{CBn}=\widehat{ABC}-\widehat{ABn}=\alpha+\beta-\alpha=\beta\)
\(\Rightarrow\widehat{CBn}=\widehat{BCy}=\beta\)
Mà 2 góc này là 2 góc so le trong
=> Cy//Bm


a) Số bê tông cần đổ là:
20.6.0,15 = 18 (m3)
b) Cần số chiếc xe để chở đủ số lượng bê tông nói trên là:
18 : 6 = 3 (xe)

a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=5^2-3^2=16\)
=>\(AC=\sqrt{16}=4\left(cm\right)\)
b: Sửa đề: ME cắt BA tại K
Xét ΔABM vuông tại A và ΔEBM vuông tại E có
BM chung
\(\widehat{ABM}=\widehat{EBM}\)
Do đó: ΔBAM=ΔBEM
c: Ta có: ΔBAM=ΔBEM
=>BA=BE
Xét ΔBEK vuông tại E và ΔBAC vuông tại A có
BE=BA
\(\widehat{EBK}\) chung
Do đó: ΔBEK=ΔBAC
=>BK=BC
=>ΔBKC cân tại B
d: Ta có: MA+MC=AC
ME+MK=KE
mà AC=KE và MA=ME
nên MK=MC
=>ΔMKC cân tại M
=>\(\widehat{KMC}=180^0-2\cdot\widehat{MKC}\)
mà \(\widehat{KMC}=\widehat{AME}\)(hai góc đối đỉnh)
nên \(\widehat{AME}=180^0-2\cdot\widehat{MKC}\left(1\right)\)
Xét tứ giác BAME có
\(\widehat{BAM}+\widehat{BEM}+\widehat{ABE}+\widehat{AME}=360^0\)
=>\(\widehat{AME}+\widehat{ABC}=180^0\)
=>\(\widehat{AME}=180^0-\widehat{ABC}\left(2\right)\)
Từ (1),(2) suy ra \(\widehat{ABC}=2\cdot\widehat{MKC}\)