Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kẻ GH⊥BC tại H
Kẻ MK⊥BC tại K
Xét ΔABC có
G là trọng tâm của ΔABC(gt)
BG cắt AC tại M(gt)
Do đó: M là trung điểm của AC
Xét ΔABC có
BM là đường trung tuyến ứng với cạnh AC(M là trung điểm của AC)
G là trọng tâm của ΔABC(gt)
Do đó: \(BG=\dfrac{2}{3}BM\)(Tính chất ba đường trung tuyến của tam giác)
Ta có: GH⊥BC(gt)
MK⊥BC(gt)
Do đó: GH//MK(Định lí 1 từ vuông góc tới song song)
Xét ΔBMC có
G∈BM(gt)
H∈BC(gt)
GH//MK(cmt)
Do đó: \(\dfrac{GH}{MK}=\dfrac{BG}{BM}\)(Hệ quả của định lí Ta lét)
mà \(\dfrac{BG}{BM}=\dfrac{2}{3}\)(cmt)
nên \(\dfrac{GH}{MK}=\dfrac{2}{3}\)
Xét ΔGBC có GH⊥BC(gt)
nên \(S_{GBC}=\dfrac{GH\cdot BC}{2}\)
Xét ΔMBC có MK⊥BC(gt)
nên \(S_{MBC}=\dfrac{MK\cdot BC}{2}\)
Ta có: \(S_{GBC}:S_{MBC}=\dfrac{GH\cdot BC}{2}:\dfrac{MK\cdot BC}{2}\)
\(\Leftrightarrow\dfrac{S_{GBC}}{S_{MBC}}=\dfrac{GH\cdot BC}{2}\cdot\dfrac{2}{MK\cdot BC}\)
\(\Leftrightarrow\dfrac{S_{GBC}}{S_{MBC}}=\dfrac{GH}{MK}=\dfrac{2}{3}\)
hay \(S_{GBC}=\dfrac{2}{3}\cdot S_{MBC}\)(đpcm)

Lời giải:
Kéo dài $BG$ cắt $AC$ tại $K$. Kẻ $KK'\perp d$
Trên $BG$ lấy trung điểm $I$. Kẻ $II'\perp d$
Vận dụng công thức đường trung bình trong hình thang ta có:
Xét hình thang $BGG'B'$ có đtb $II'$ thì:
$II'=\frac{BB'+GG'}{2}(1)$
Xét hình thang $AA'C'C$ có đường trung bình $KK'$ thì:
$KK'=\frac{AA'+CC'}{2}(2)$
Xét hình thang $II'KK'$ có đường trung bình $GG'$ thì:
$GG'=\frac{II'+KK'}{2}(3)$
Từ $(1);(2);(3)$ suy ra:
$GG'=\frac{BB'+GG'+AA'+CC'}{4}$
$\Rightarrow GG'=\frac{AA'+BB'+CC'}{3}$
Ta có đpcm.

Gọi M là trung điểm của BC, D là chân đường phân giác kẻ từ A xuống BC
=>A,G,M thẳng hàng và A,I,D thẳng hàng
BM=CM=BC/2=7,5cm
AD là phân giác
=>BD/AB=CD/AC
=>BD/4=CD/6=15/10=1,5
=>BD=6cm
=>MD=1,5cm
IG//DM
=>IG/DM=AI/AD=2/3
=>IG=2/3DM=1cm

Ai Đó Không Phải Anh,Ai Đó Không Phải Anh,Ai Đó Không Phải Anh,Ai Đó Không Phải Anh,Ai Đó Không Phải Anh,Ai Đó Không Phải Anh,Ai Đó Không Phải Anh,Ai Đó Không Phải Anh,Ai Đó Không Phải Anh,Ai Đó Không Phải Anh,
ghghhggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggghhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhh
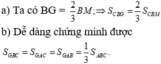
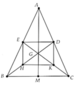
a) G là trọng tâm của \(\Delta\)ABC nên M
là trung điểm của AC và BG = \(\dfrac{2}{3}BM\)
SGBC = \(\dfrac{2}{3}s_{MBC}\) (2 tam giác GBC , MBC chung đường cao vẽ từ C đến BM và BG =\(\dfrac{2}{3}BM\))
b) SMBC = \(\dfrac{1}{2}s_{ABC}\) ( 2 tam giác MBC , ABC chung đường cao vẽ từ B đến AC, MC = \(\dfrac{1}{2}AC\))
Mà SMBC =\(\dfrac{2}{3}S_{MBC}\) ( câu a ). Do đó SGBC =\(\dfrac{2}{3}.\dfrac{1}{2}S_{MBC}\) = \(\dfrac{1}{3}S_{ABC}\)
Tương tự có SGAB = \(\dfrac{1}{3}S_{ABC}\) , SGAB =\(\dfrac{1}{3}S_{ABC}\)