Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

* Ta có:
f(x) = x5 – 3x2 + 7x4 – 9x3 + x2 - 1/4 x
= x5 – (3x2 – x2) + 7x4 – 9x3 -1/4.x
= x5 – 2x2 + 7x4 – 9x3 -1/4.x
= x5 + 7x4 – 9x3 – 2x2 - 1/4
g(x) = 5x4 – x5 + x2 – 2x3 + 3x2 - 1/4
= 5x4 –x5+ (x2 + 3x2) – 2x3 – 1/4
= 5x4 – x5 + 4x2 – 2x3 – 1/4
= -x5 + 5x4 – 2x3 + 4x2 - 1/4
* f(x) + g(x)
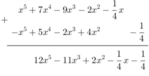
* f(x) - g(x)
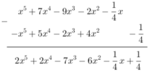

a) Sắp xếp theo lũy thừa giảm dần
P(x)=x^5−3x^2+7x^4−9x^3+x^2−1/4x
=x^5+7x^4−9x^3−3x^2+x^2−1/4x
=x^5+7x^4−9x^3−2x^2−1/4x
Q(x)=5x^4−x^5+x^2−2x^3+3x^2−1/4
=−x^5+5x^4−2x^3+x^2+3x^2−1/4
=−x^5+5x^4−2x^3+4x^2−1/4
b)
P(x)+Q(x)
=(x^5+7x^4−9x^3−2x^2−1/4^x)+(−x^5+5x^4−2x^3+4x^2−1/4)
=x^5+7x^4−9x^3−2x^2−1/4x−x^5+5x^4−2x^3+4x^2−1/4
=(x^5−x^5)+(7x^4+5x^4)+(−9x^3−2x^3)+(−2x^2+4x^2)−1/4x−1/4
=12x^4−11x^3+2x^2−1/4x−1/4
P(x)−Q(x)
=(x^5+7x^4−9x^3−2x^2−1/4x)−(−x^5+5x^4−2x^3+4x^2−1/4)
=x^5+7x^4−9x^3−2x^2−1/4x+x^5−5x^4+2x^3−4x^2+1/4
=(x^5+x^5)+(7x^4−5x^4)+(−9x^3+2x^3)+(−2x^2−4x^2)−1/4x+1/4
=2x5+2x4−7x3−6x2−1/4x−1/4
c) Ta có
P(0)=0^5+7.0^4−9.0^3−2.0^2−1/4.0
⇒x=0là nghiệm của P(x).
Q(0)=−0^5+5.0^4−2.0^3+4.0^2−1/4=−1/4≠0
⇒x=0không phải là nghiệm của Q(x).
Cho 2 đa thức: f(x)= 9 - x5 + 4x - 2x3 + x2 - 7x4
g(x)= x5 - 9 + 2x2 + 7x4 + 2x3 - 3x
a) Sắp sếp các đa thức trên theo luỹ thừa giảm dần của biến
f(x)= 9 - x5 + 4x - 2x3 + x2 - 7x4
f(x) = -x5 - 7x4 - 2x3 + x2 + 4x + 9
g(x)= x5 - 9 + 2x2 + 7x4 + 2x3 - 3x
g(x) = x5 + 7x4 + 2x3 + 2x2 - 3x - 9
b) Tìm bậc, hệ số cao nhất, hệ số tự do của đa thức f(x); g(x)
f(x) = -x5 - 7x4 - 2x3 + x2 + 4x + 9
+ Bậc : 5 _ hệ số cao nhất : -1 _ hệ số tự do : 9
g(x) = x5 + 7x4 + 2x3 + 2x2 - 3x - 9
+ Bậc : 5_ hệ số cao nhất : 1 _ hệ số tự do : -9
c) Tính f(x) + g(x); f(x) - g(x)
f( x) + g(x) = ( -x5 - 7x4 - 2x3 + x2 + 4x + 9 ) +( x5 + 7x4 + 2x3 + 2x2 - 3x - 9 )
= -x5 - 7x4 - 2x3 + x2 + 4x + 9 + x5 + 7x4 + 2x3 + 2x2 - 3x - 9
= ( -x5 + x5 ) + ( -7x4 + 7x4 ) + ( -2x3 + 2x3 ) + ( x2 + 2x2 ) + ( 4x -3x ) + ( 9 - 9 )
= 3x2 + x
f( x) - g(x) = ( -x5 - 7x4 - 2x3 + x2 + 4x + 9 ) - ( x5 + 7x4 + 2x3 + 2x2 - 3x - 9 )
= -x5 - 7x4 - 2x3 + x2 + 4x + 9 - x5 - 7x4 - 2x3 - 2x2 + 3x + 9
= ( -x5 - x5 ) + ( -7x4 - 7x4 ) + ( -2x3 - 2x3 ) + ( x2 - 2x2 ) + ( 4x + 3x ) + ( 9 + 9 )
= -2x5 - 14x4 - 2x3 -x2 + 7x + 18

b)
Sửa đề: f(x)=A(x)+B(x)
Ta có: f(x)=A(x)+B(x)
\(=x^5+7x^4-9x^3-2x^2-\dfrac{1}{4}x-x^5+5x^4-2x^3+4x^2-\dfrac{1}{4}\)
\(=12x^4-11x^3+2x^2-\dfrac{1}{4}x-\dfrac{1}{4}\)
a) Ta có: \(A\left(x\right)=x^5-3x^2+7x^4-9x^3+x^2-\dfrac{1}{4}x\)
\(=x^5+7x^4-9x^3+\left(-3x^2+x^2\right)-\dfrac{1}{4}x\)
\(=x^5+7x^4-9x^3-2x^2-\dfrac{1}{4}x\)
Ta có: \(B\left(x\right)=5x^4-x^5+x^2-2x^3+3x^2-\dfrac{1}{4}\)
\(=-x^5+5x^4-2x^3+\left(x^2+3x^2\right)-\dfrac{1}{4}\)
\(=-x^5+5x^4-2x^3+4x^2-\dfrac{1}{4}\)

Ta đặt và thực hiện các phép tính P(x) + Q(x) và P(x) – Q(x).

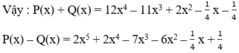

a, Ta có : \(h\left(x\right)=f\left(x\right)+g\left(x\right)\)
hay \(h\left(x\right)=-x^5-7x^4-2x^3+x^2+4x+9+x^5+7x^4+2x^3+2x^2-3x-9\)
\(h\left(x\right)=3x^2+x\)
b, Đặt \(3x^2+x=0\Leftrightarrow x\left(3x+1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{1}{3}\end{matrix}\right.\)
Vậy nghiệm của đa thức h(x) là x = -1/3 ; x = 0
c, Ta có : \(k\left(x\right)=f\left(x\right)-g\left(x\right)\)
hay \(k\left(x\right)=-x^5-7x^4-2x^3+x^2+4x+9-x^5-7x^4-2x^3-2x^2+3x+9\)
\(k\left(x\right)=-2x^5-14x^4-4x^3-x^2+7x+18\)
f(x)=-x5-7x4 -2x3+x2+4x+9
g(x)=x5+7x4+2x3+2x2-3x-9
Tính
a)h(x)=f(x)+g(x)
Ta có: h(x) = f(x) + g(x)
= (-x5-7x4 -2x3+x2+4x+9) + (x5+7x4+2x3+2x2-3x-9)
= (x5-x5) + (7x4-7x4) + (2x3-2x3) + (x2+2x2)+ (4x-3x) + (9-9)
=3x2+x
b)Tìm nghiệm của h(x)
h(x) = 0 <=> 3x2+x= 0
<=> x(3x+1) =0 <=> x= 0 hoặc x =-1/3
Vậy nghiệm của h(x) là x thuộc {0;-1/3}
c)k(x)=f(x)-g(x)
=(-x5-7x4 -2x3+x2+4x+9) - (x5+7x4+2x3+2x2-3x-9)
= (-x5-x5) + (-7x4-7x4) + (-2x3-2x3) + (x2-2x2) (4x+3x) + (9+9)
=-2x5-14x4 -4x3-x2+7x+19


Ta có: f(0) = 05 - 3.02 + 7.04 - 9.03 + 02 - 1/4.0 = 0
=> x = 0 là nghiệm của f(x)
g(0) = 5.04 - 05 + 02 - 2.03 + 3.02 - 1/4 = -1/4 \(\ne\)0
=> x = 0 ko là nghiệm của g(x)
Vậy x = 0 là nghiệm của f(x) những ko là nghiệm của g(x)
Câu hỏi của chị ,em ko có biêt́ .Em hoc lop 5 hihi
mà nếu thấy em thì chị kêt́ bạn voi em nhé !!!!!!