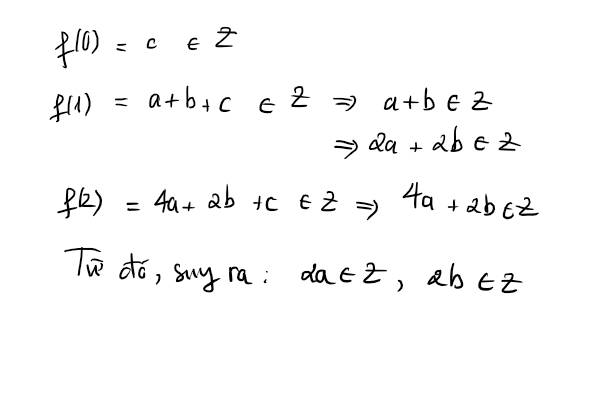Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) f(0) = c; f(0) nguyên => c nguyên (*)
f(1) = a+ b + c ; f(1) nguyên => a+ b + c nguyên (**)
f(2) = 4a + 2b + c ; f(2) nguyên => 4a + 2b + c nguyên (***)
Từ (*)(**)(***) => a + b và 4a + 2b nguyên
4a + 2b = 2a + 2.(a + b) có giá trị nguyên mà 2(a+ b) nguyên do a+ b nguyên
nên 2a nguyên => 4a có giá trị nguyên mà 4a + 2b nguyên do đó 2b có giá trị nguyên
b) f(3) = 9a + 3b + c = (a+ b + c) + (4a + 2b) + 4a
Vì a+ b + c ; 4a + 2b; 4a đều có giá trị nguyên nên f(3) có giá trị nguyên
f(4) = 16a + 4b + c = (a+ b) + (9a + 3b + c) + 3. 2a
Vì a+ b; 9a + 3b + c; 2a đều nguyên nên f(4) có giá trị nguyên
f(5) = 25a + 5b + c = (16a + 4b + c) + (a+ b) + 4. 2a
Vì 16a + 4b + c ; a+ b; 2a đều có giá trị nguyên nên f(5) có giá trị nguyên

Ta có:
\(f\left(0\right)=c\in Z\)(1)
\(f\left(1\right)=a+b+c\in Z\)(2)
\(f\left(2\right)=4a+2b+c\in Z\)(3)_
Từ (1), (2) => \(a+b\in Z\)=> \(2a+2b\in Z\)(4)
Từ (1), (3)=> 4a+2b\(\in Z\)(5)
Từ (4), (5) => \(\left(4a+2b\right)-\left(2a+2b\right)\in Z\)
=> \(2a\in Z\)=> \(2b\in Z\)

*f(0) nguyên suy ra 0+0+c=c nguyên
*Vì c nguyên và f(1)=a+b+c nguyên suy ra a+b nguyên
*Tương tự vs f(2)=4a+2b+c suy ra 2a nguyên (Vì 4a+2b và 2(a+b) đều nguyên)
Vì 2a và 2(a+b) nguyên suy ra 2b nguyên (đpcm)

\(f\left(0\right)=a.0^2+b.0+c=c\) có giá trị nguyên
\(f\left(1\right)=a+b+c\) có giá trị nguyên => a + b có giá trị nguyên
\(f\left(2\right)=4a+2b+c=2a+2\left(a+b\right)+c\)=> 2a có giá trị nguyên
=> 4a có giá trị nguyên
=> 2b có giá trị nguyên.

Lời giải:
$f(0)=a.0^2+b.0+c=c$ nguyên
$f(1)=a+b+c$ nguyên, mà $c$ nguyên nên $a+b+c-c=a+b$ nguyên
$f(2)=4a+2b+c=2a+2(a+b)+c$ nguyên mà $a+b, c$ nguyên nên $2a$ nguyên
$2a$ nguyên, $2(a+b)$ nguyên nên $2b$ nguyên.
Ta có đpcm.

) f(0) = c; f(0) nguyên => c nguyên (*)
f(1) = a+ b + c ; f(1) nguyên => a+ b + c nguyên (**)
f(2) = 4a + 2b + c ; f(2) nguyên => 4a + 2b + c nguyên (***)
Từ (*)(**)(***) => a + b và 4a + 2b nguyên
4a + 2b = 2a + 2.(a + b) có giá trị nguyên mà 2(a+ b) nguyên do a+ b nguyên
nên 2a nguyên => 4a có giá trị nguyên mà 4a + 2b nguyên do đó 2b có giá trị nguyên
:3
Có \(f\left(0\right);f\left(1\right);f\left(2\right)\)\(\in Z\Rightarrow\hept{\begin{cases}f\left(0\right)=c\in Z\\f\left(1\right)=a+b+c\in z\\f\left(2\right)=4a+2b+c\in z\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}a+b\in z\\4a+2b\in z\end{cases}\Rightarrow\hept{\begin{cases}2a+2b\in z\\4a+2b\in z\end{cases}}\Rightarrow2a\in z;}2b\in z\)
\(\RightarrowĐPCM\)