LT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
17 tháng 11 2016
Ta có
\(\frac{a^2}{b+c}+\frac{b^2}{a+c}+\frac{c^2}{a+b}\ge\frac{\left(a+b+c\right)^2}{2\left(a+b+c\right)}=1\)
Đạt được khi a = b = c = \(\frac{2}{3}\)
NH
0
30 tháng 6 2023
a: |2x|=x-4
TH1: x>=0
=>2x=x-4
=>x=-4(loại)
TH2: x<0
=>-2x=x-4
=>-3x=-4
=>x=4/3(loại)
b: 7-|2x+1|=x
=>|2x+1|=7-x
TH1: x>=-1/2
=>2x+1=7-x
=>3x=6
=>x=2(nhận)
TH2: x<-1/2
=>2x+1=x-7
=>x=-8(nhận)
Y
30 tháng 6 2023
\(\left|2x\right|=x-4\)
\(TH_1:x\ge0\\ 2x=x-4\Leftrightarrow2x-x=-4\Leftrightarrow x=-4\left(ktm\right)\)
\(TH_2:x< 0\\\Leftrightarrow-2x=x-4\Leftrightarrow-2x-x=-4\Leftrightarrow-3x=-4\Leftrightarrow x=\dfrac{4}{3}\left(ktm\right) \)
Vậy pt vô nghiệm.
\(7-\left|2x+1\right|=x\\ \Leftrightarrow\left|2x+1\right|=7-x\)
\(TH_1:x\ge-\dfrac{1}{2}\)
\(2x+1=7-x\Leftrightarrow2x+x=7-1\Leftrightarrow3x=6\Leftrightarrow x=2\left(tm\right)\)
\(TH_2:x< -\dfrac{1}{2}\\ -2x-1=7-x\Leftrightarrow-2x+x=7+1\Leftrightarrow-x=8\Leftrightarrow x=-8\left(tm\right)\)
Vậy \(S=\left\{-8;2\right\}\)
CH
Cô Hoàng Huyền
Admin
VIP
27 tháng 6 2016
Dạng tổng quát:
Muốn tính giá trị của f(a), ta tách : f(a) = g(a).t(a) + h(a) sao cho g(a) = 0. Khi đó ta có: f(a) = h(a) với h(x) là phần dư của phép chia f(x) cho g(x).
Khi làm nhiều ta nhẩm được pt bậc hai nhận nghiệm \(-2+\sqrt{5}\) là pt \(x^2+4x-1=0\)
NH
1
KN
10 tháng 9 2019
\(4t^2+20t+x=0\)
\(\Leftrightarrow\left(2t\right)^2+2.2t.5+x=0\)
Vậy x = \(5^2=25\)
TA
1 tháng 7 2017
a) \(\frac{1}{x_1^2}+\frac{1}{x_2^2}=\frac{x_1^2+x_2^2}{x_1^2x_1^2}=\frac{\left(x_1+x_2\right)^2-2x_1x_2}{\left(x_1x_2\right)^2}\)
b) \(x_1^3+x_2^3=\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)\)
Đến đây bn tự xài Viet đc rồi nhé
KT
10 tháng 7 2018
a) Áp dụng BĐT AM-GM ta có:
\(x+y\ge2\sqrt{xy}\)
\(\Rightarrow\)\(\frac{x+y}{2}\ge\sqrt{xy}\)
Dấu "=" xảy ra \(\Leftrightarrow\)\(x=y\)
b) Áp dụng BĐT AM-GM ta có:
\(\frac{\sqrt{x}}{\sqrt{y}}+\frac{\sqrt{y}}{\sqrt{x}}\ge2\sqrt{\frac{\sqrt{x}}{\sqrt{y}}.\frac{\sqrt{y}}{\sqrt{x}}}=2\)
Dấu "=" xảy ra \(\Leftrightarrow\)\(x=y\)
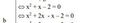
\(x^2+2x-x-2=x^2+\left(2x-x\right)-2=x^2+x-2\)