Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1 : Bài giải
Hình tự vẽ //
a) Ta có DOC = cung DC
Vì DOC là góc ở tâm và DAC là góc chắn cung DC
=>DOC = 2 . AOC (1)
mà tam giác AOC cân =>AOC=180-2/AOC (2)
Từ (1) ; (2) ta được DOC + AOC = 180
b) Góc ACD là góc nội tiếp chắn nữa đường tròn
=>ACD=90 độ
c) c) HC=1/2*BC=12
=>AH=căn(20^2-12^2)=16
Ta có Sin(BAO)=12/20=>BAO=36.86989765
=>AOB=180-36.86989765*2=106.2602047
Ta có AB^2=AO^2+OB^2-2*OB*OA*cos(106.2602047)
<=>AO^2+OA^2-2OA^2*cos(106.2602047)=20^2
=>OA=12.5

a) có: A1C.vtA1B + A1B.vtA1C =vt0 (*)
mặt khác do tính chất phân giác ta có: c/A1B = b/A1C => A1C = b.A1B/c
thay vào (*): (b.A1B/c).vtA1B + A1B.vtA1C = vt0
<=> (b/c).vtA1B + vtA1C = vt0
<=> b.vtA1B + c.vtA1C= vt0
2QP = QA + QD = QC + CA + QB + BD = CA + BD
=> 2QP.MN = (CA + BD)MN = CA.MN + BD.MN =
= CA.(MB + BN) + BD.(MC + CN)
= CA.MB + CA.BN + BD.MC + BD.CN
= CA.BN + BD.MC (vì CA_|_MB, BD_|_CN nên có hai cái = 0)
= CA.(BD+DN) + BD.(MA+AC)
= CA.BD + CA.DN + BD.MA + BD.AC
= BD.(CA+AC) + 0 + 0 = 0 (CA_|_DN và BD_|_MA)
Có vtQP.vtMN = 0 <=> QP _|_ MN
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)

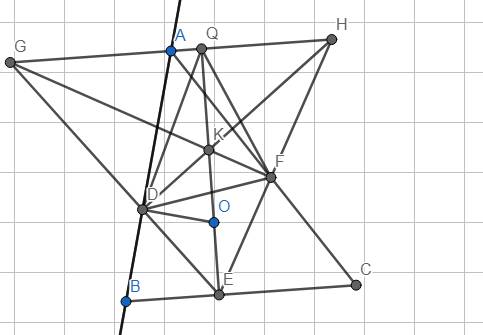
1) Vì \(\left(O\right)\) nội tiếp △ABC và tiếp xúc với AB,BC,CA lần lượt tại D,E,F.
\(\Rightarrow\left\{{}\begin{matrix}BE=BD\\AD=AF\\CE=CF\end{matrix}\right.\) và \(\left\{{}\begin{matrix}OD\perp ABtạiD\\OE\perp BCtạiE\\OF\perp CAtạiF\end{matrix}\right.\)
\(BD+BE=AB-AD+BC-CE=AB+BC-AF-CF=AB+BC-CA\)
\(\Rightarrow2BD=c+a-b\)
\(\Rightarrow BD=\dfrac{c+a-b}{2}\)
\(\Rightarrow AD=AB-BD=c-\dfrac{c+a-b}{2}=\dfrac{c+b-a}{2}\)
\(\Rightarrow\dfrac{AD}{BD}=\dfrac{\dfrac{c+b-a}{2}}{\dfrac{c+a-b}{2}}=\dfrac{c+b-a}{c+a-b}\)
Xét △BDE có: BE//AG.
\(\Rightarrow\dfrac{DG}{DE}=\dfrac{AD}{BD}=\dfrac{c+b-a}{c+a-b}\) (định lí Ta-let).
2) \(BD=BE\Rightarrow\)△BDE cân tại B.
\(\Rightarrow\widehat{BDE}=\widehat{BED}\) mà \(\left\{{}\begin{matrix}\widehat{BDE}=\widehat{ADG}\\\widehat{BED}=\widehat{AGD}\end{matrix}\right.\)
\(\Rightarrow\widehat{ADG}=\widehat{AGD}\Rightarrow\)△ADG cân tại A.
\(\Rightarrow AD=AG=AF\)
Tương tự \(AH=AF\Rightarrow AG=AH\)
\(\Rightarrow\)A là trung điểm GH.
\(\Rightarrow DA=DF=AG=\dfrac{1}{2}GH\)
△DHG có: DA là trung tuyến và \(DA=\dfrac{1}{2}GH\)
\(\Rightarrow\)△DHG vuông tại D.
\(\Rightarrow\)HD là đường cao của △GHE (1).
Tương tự: GF là đường cao của △GHE (2).
Ta có \(OE\perp BC\) mà BC//GH \(\Rightarrow OE\perp GH\)
\(\Rightarrow\)OE là đường cao của △GHE (3).
(1),(2),(3) \(\Rightarrow\)GF, HD, OE đồng quy.
3) \(EO\perp GH\) tại Q.
Gọi K là trực tâm của △GHE.
Vì △KDE, △KFE nội tiếp đường tròn đường kính KE nên:
K,D,E,F cùng thuộc 1 đường tròn.
Mà \(D,E,F\in\left(O\right)\Rightarrow K\in\left(O\right)\).
Chứng minh K là tâm đường tròn nội tiếp △DFQ \(\Rightarrow\)Sử dụng tam giác đồng dạng và tính chất 3 đg cao trong △DFQ.

a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
Gọi H là giao điểm của FM và OA.
Tính được \(AM=\dfrac{b+c-a}{2}\)
Tính được \(cos\widehat{BAC}=\dfrac{b^2+c^2-a^2}{2bc}\) rồi dùng
\(MF=\sqrt{AM^2+AF^2-2AM.AF.cos\widehat{BAC}}\)
\(=\sqrt{2AM^2\left(1-cos\widehat{BAC}\right)}\)
\(=MA\sqrt{2\left(1-\dfrac{b^2+c^2-a^2}{2bc}\right)}\)
\(=MA\sqrt{\dfrac{a^2-\left(b-c\right)^2}{bc}}\)
\(=\dfrac{b+c-a}{2}\sqrt{\dfrac{a^2-\left(b-c\right)^2}{bc}}\)
\(\Rightarrow\dfrac{MF}{MA}=\sqrt{\dfrac{a^2-\left(b-c\right)^2}{bc}}=J\)
\(\Rightarrow cos\widehat{MEF}=cos\widehat{MAH}=\dfrac{MH}{MA}=\dfrac{J}{2}\)
\(\Rightarrow sin\widehat{MEF}=\sqrt{1-cos^2\widehat{MAH}}\)
\(=\sqrt{1-\dfrac{J^2}{4}}\)
\(=\sqrt{1-\dfrac{a^2-b^2-c^2+2bc}{4bc}}\)
\(=\sqrt{\dfrac{\left(b+c\right)^2-a^2}{4bc}}\) \(=A\)
Ta cũng tính được \(ME=\dfrac{c+a-b}{2}\sqrt{\dfrac{b^2-\left(c-a\right)^2}{ca}}=\dfrac{c+a-b}{2}\sqrt{\dfrac{\left(b+c-a\right)\left(a+b-c\right)}{ca}}\)
\(EF=\dfrac{a+b-c}{2}\sqrt{\dfrac{c^2-\left(a-b\right)^2}{ab}}=\dfrac{a+b-c}{2}\sqrt{\dfrac{\left(c+a-b\right)\left(b+c-a\right)}{ab}}\)
\(\Rightarrow S_{MEF}=\dfrac{1}{2}EM.EF.sin\widehat{MEF}\) \(=...\)