Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Tiếp tuyến AM vuông góc với bán kính đường tròn (O) tại tiếp điểm M
hay tam giác OMA vuông tại M
Dễ thấy AM = \(\sqrt{ }\)(OA^2 - OM^2)= 4 (cm) (Pythagores)
Vậy AM = AN = 4cm.
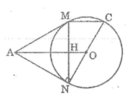
Ta có: AN ⊥ NC (tính chất tiếp tuyến)
Áp dụng định lí Pitago vào tam giác vuông AON ta có :
A O 2 = A N 2 + O N 2
Suy ra : A N 2 = A O 2 - O N 2 = 5 2 - 3 2 = 16
AN = 4 (cm)
Suy ra: AM = AN = 4 (cm)
Gọi H là giao điểm của AO và MN
Ta có: MH = NH = MN/2 (tính chất tam giác cân)
Tam giác AON vuông tại N có NH ⊥ AO. Theo hệ thức lượng trong tam giác vuông, ta có:
OA.NH = AN.ON ⇒ NH = (AN.ON)/AO = (4.3)/5 = 2,4 (cm)
MN = 2.NH = 2.2,4 = 4,8 (cm)
a,theo t/c 2 tiếp tuyến cắt nhau thì \(MA=NA\Rightarrow\Delta AMN\) cân và \(OA\) la p/g cua goc MAN \(\Rightarrow AO\) là dg p/g đóng vai vai trò đg cao \(\Rightarrow AO\perp MN\)
b,tam giác CMN có CN là đg kính nên tam giác CMN là tam giác vuông nên goc CMO +goc OMN =90 mat khác góc OMN+góc AOM =90 (MN \(\perp\) OA)\(\Rightarrow\)góc CMO =goc AOM(cùng phụ góc OMN) ở vị trí so le trong nên MC song song voi AO
C,xet \(\Delta OMA\) có \(AM=\sqrt{OA^2-OM^2}=\sqrt{5^2-3^2}=4\Rightarrow AN=AM=4\)
va MH=\(\frac{MA.MO}{OA}=\frac{4.3}{5}=2.4\Rightarrow MN=2MH=4.8\)
mình làm có gì sai mong bạn bỏ qua
format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22math11ce3e6e3f452828e23a0c94572%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%228.5%22%20y%3D%2216%22%3E%26%23x22A5%3B%3C%2Ftext%3E%3C%2Fsvg%3E)
MN
b) Vẽ đường kính NOC. Chứng minh: MC // AO
c) Tính chu vi format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22math1ed582716bfb4738ccd92405301%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%227.5%22%20y%3D%2216%22%3E%26%23x2206%3B%3C%2Ftext%3E%3C%2Fsvg%3E)
AMN biết OM= 3cm và OA = 5cm
a) Xét (O) có
AM là tiếp tuyến có M là tiếp điểm(gt)
AN là tiếp tuyến có N là tiếp điểm(gt)
Do đó: AM=AN; OM=ON(Tính chất hai tiếp tuyến cắt nhau)
Ta có: AM=AN(cmt)
nên A nằm trên đường trung trực của MN(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: OM=ON(cmt)
nên O nằm trên đường trung trực của MN(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AO là đường trung trực của MN
hay AO⊥MN(đpcm)
b) Xét (O) có
ΔMNC nội tiếp đường tròn(C,M,N∈(O))
NC là đường kính
Do đó: ΔMNC vuông tại M(Định lí)
⇒MN⊥MC
Ta có: MN⊥MC(cmt)
MN⊥AO(cmt)
Do đó: MC//AO(Định lí 1 từ vuông góc tới song song)
c) Áp dụng định lí Pytago vào ΔOMA vuông tại M, ta được:
\(OA^2=OM^2+MA^2\)
\(\Leftrightarrow AM^2=OA^2-OM^2=5^2-3^2=16\)
hay \(AM=\sqrt{16}=4cm\)
mà AM=AN(cmt)
nên AN=4cm
Gọi H là giao điểm của MN và AO
mà MN⊥AO tại trung điểm của MN
nên H là trung điểm của MN và MH⊥AO tại H
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAMO vuông tại M, ta được:
\(MH\cdot AO=MO\cdot MA\)
\(\Leftrightarrow MH\cdot5=4\cdot3=12\)
hay MH=2,4cm
mà \(MN=2\cdot MH\)(H là trung điểm chung của MN)
nên \(MN=2\cdot2.4=4.8cm\)
Chu vi tam giác AMN là:
\(C=AM+AN+MN=5+5+4.8=14.8cm\)
Cho sửa lại đề tí ==* , câu b) là c/m MR // AO => MC // AO :>
a. Ta có: AM = AN (tính chất hai tiếp tuyến cắt nhau)
Suy ra tam giác AMN cân tại A
Mặt khác AO là đường phân giác của góc MAN ( tính chất hai tiếp tuyến cắt nhau )
Suy ra AO là đường cao của tam giác AMN ( tính chất tam giác cân )
Vậy \(OA\perp MN\)
b. Tam giác MNC nội tiếp trong đường tròn (O) có NC là đường kính nên góc (CMN) = 90o
Suy ra: \(NM\perp MC\)
Mà \(OA\perp MN\)(chứng minh trên)
Suy ra: OA // MC
c. Ta có: \(AN\perp NC\) (tính chất tiếp tuyến)
Áp dụng định lí Pitago vào tam giác vuông AON ta có :
AO2 = AN2 + ON2
Suy ra : AN2 = AO2 – ON2 = 52 – 32 = 16
AN = 4 (cm)
Suy ra: AM = AN = 4 (cm)
Gọi H là giao điểm của AO và MN
Ta có: \(MH=NH=\frac{MN}{2}\) (tính chất tam giác cân)
Tam giác AON vuông tại N có \(NH\perp AO\). Theo hệ thức lượng trong tam giác vuông, ta có:
OA . NH = AN . ON => \(NH=\frac{\left(AN.ON\right)}{AO}=\frac{\left(4.3\right)}{5}=2,4\)
MN = 2.NH = 2.2,4 = 4,8 (cm)
Vậy .....................
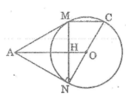
Ta có: AM = AN (tính chất hai tiếp tuyến cắt nhau)
Suy ra tam giác AMN cân tại A
Mặt khác AO là đường phân giác của góc MAN (tính chất hai tiếp tuyến cắt nhau)
Suy ra AO là đường cao của tam giác AMN (tính chất tam giác cân)
Vậy OA ⊥ MN.
a) ta có : AN = AM (tính chất tiếp tuyến)
\(\Rightarrow\) tam giác AMN cân tại A
OA là tia phân giác cũng là đường cao
\(\Rightarrow\) OA \(\perp\) MN (đpcm)
b) đặc H là giao điểm của MN và AO
ta có MH = HN (OA \(\perp\) MN \(\Rightarrow\) H là trung điểm MN)
mà CO = CN = R
\(\Rightarrow\) OH là đường trung bình của tam giác MNC
\(\Rightarrow\) OH // MC \(\Leftrightarrow\) MC // OA (đpcm)