Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

 ∆OBH vuông tại H
∆OBH vuông tại H
⇒ OB² = OH² + BH² (Pytago)
⇒ BH² = OB² - OH²
= 5² - 4²
= 9
⇒ BH = 3 (cm)
Do OH ⊥ AB
⇒ H là trung điểm của AB
⇒ AB = 2BH = 2.3 = 6 (cm)
Gọi OH là khoảng cách từ tâm O đến dây AB
=>OH\(\perp\)AB tại H
=>OH=4cm
ΔOAB cân tại O
mà OH là đường cao
nên H là trung điểm của AB
ΔOHA vuông tại H
=>\(OH^2+HA^2=OA^2\)
=>\(HA^2+4^2=5^2\)
=>\(HA^2=5^2-4^2=9\)
=>HA=3(cm)
H là trung điểm của AB
=>\(AB=2\cdot AH=6\left(cm\right)\)

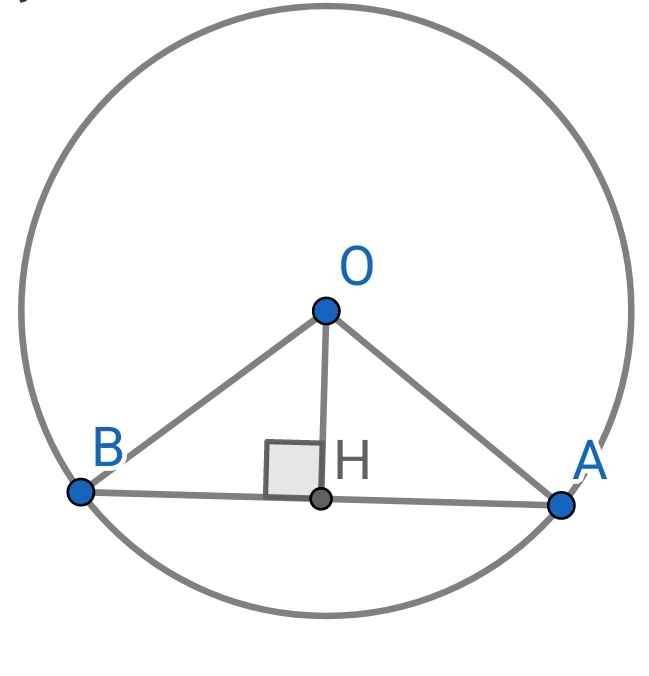
∆OBH vuông tại H
⇒ OB² = OH² + BH² (Pytago)
⇒ BH² = OB² - OH²
= 13² - 5²
= 144
⇒ BH = 12 (cm)
⇒ AB = 2BH = 2.12 = 24 (cm)
Chọn C

Xét tam giác OAB
Chu vi C = 10 + 10 + 12 = 32 cm
p = C/2 = 32/2 = 16 cm
SOAB = \(\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\)
= \(\sqrt{16\left(16-10\right)\left(16-10\right)\left(16-12\right)}\)
= \(\sqrt{16.6.6.4}\)
= 4.6.2 = 48 cm2
SOAB = \(\frac{1}{2}\)AB.h
=> h = 2SOAB/AB = 48.2/12 = 8 cm

Mình sẽ không vẽ hình vì sợ duyệt.
Vì (O) có bán kính 10cm nên \(OA=10cm\)
Gọi OH là khoảng cách từ O đến AB, khi đó theo quan hệ vuông góc giữa đường kính và dây, ta có H là trung điểm AB, từ đó \(AB=2AH\)
Đồng thời, \(OH=8cm\)
\(\Delta OAH\)vuông tại H \(\Rightarrow AH=\sqrt{OA^2-OH^2}=\sqrt{10^2-8^2}=6\left(cm\right)\)
\(\Rightarrow AB=2AH=2.6=12\left(cm\right)\)
\(\Rightarrow\)Chọn A
C
Chọn C