Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét \(\Delta\)AOB vuông tại B có
\(\cos\widehat{AOB}=\dfrac{OB}{OA}\)(Tỉ số lượng giác góc nhọn)
\(\Leftrightarrow\cos\widehat{AOB}=\dfrac{R}{2\cdot R}=\dfrac{1}{2}\)
hay \(\widehat{AOB}=60^0\)
Vậy: \(\widehat{AOB}=60^0\)
b) Ta có: ΔOBA vuông tại B(OB⊥BA)
nên \(\widehat{AOB}+\widehat{BAO}=90^0\)(hai góc nhọn phụ nhau)
hay \(\widehat{BAO}=30^0\)
Xét (O) có
AB là tiếp tuyến có B là tiếp điểm(gt)
AC là tiếp tuyến có C là tiếp điểm(gt)
Do đó: AO là tia phân giác của \(\widehat{BAC}\)(Tính chất hai tiếp tuyến cắt nhau)
⇒\(\widehat{BAO}=\widehat{CAO}\)
hay \(\widehat{CAO}=30^0\)
Ta có: \(\widehat{CAO}+\widehat{MAO}=\widehat{MAC}\)(Vì tia AO nằm giữa hai tia AM,AC)
hay \(\widehat{MAO}=60^0\)
Xét ΔMOA có
\(\widehat{MAO}=60^0\)(cmt)
\(\widehat{MOA}=60^0\)(\(\widehat{AOB}=60^0\))
Do đó: ΔMOA đều(Dấu hiệu nhận biết tam giác đều)
⇒MA=MO(đpcm)
c) Ta có: ΔOBA vuông tại B(OB⊥BA)
mà BI là đường trung tuyến ứng với cạnh huyền OA(I là trung điểm của OA)
nên \(BI=\dfrac{OA}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
mà \(AI=\dfrac{OA}{2}\)(I là trung điểm của OA)
nên BI=AI(1)
Ta có: ΔOCA vuông tại C(OC⊥CA)
mà CI là đường trung tuyến ứng với cạnh huyền OA(I là trung điểm của OA)
nên \(CI=\dfrac{OA}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
mà \(AI=\dfrac{AO}{2}\)(I là trung điểm của OA)
nên CI=AI(2)
Từ (1) và (2) suy ra IA=IB=IC
hay I là giao điểm 3 đường trung trực của ΔABC
Xét (O) có
AB là tiếp tuyến có B là tiếp điểm(gt)
AC là tiếp tuyến có C là tiếp điểm(gt)
Do đó: AB=AC(Tính chất hai tiếp tuyến cắt nhau)
Ta có: \(\widehat{BAC}=\widehat{BAO}+\widehat{CAO}\)(tia AO nằm giữa hai tia AB,AC)
hay \(\widehat{BAC}=60^0\)
Xét ΔABC có AB=AC(cmt)
nên ΔABC cân tại A(Định nghĩa tam giác cân)
Xét ΔABC cân tại A có \(\widehat{BAC}=60^0\)(cmt)
nên ΔABC đều(Dấu hiệu nhận biết tam giác đều)
Xét ΔABC đều có I là giao điểm 3 đường trung trực của tam giác(cmt)
mà trong tam giác đều, giao điểm 3 đường trung trực cũng chính là giao điểm của 3 đường phân giác(Định lí tam giác đều)
nên I là giao điểm của 3 đường phân giác trong ΔBAC
hay I là tâm đường tròn nội tiếp ΔABC(đpcm)

a: Phải vì góc này tạo bởi tiếp tuyến MA và day cung AB
b: Xét ΔMOA vuông tại A có cosMOA=OA/OM=1/2
=>góc MOA=60 độ
sđ cung AB=2*60=120 độ
c: Xét (O) có
MA,MB là tiếp tuyến
=>MA=MB
mà OA=OB
nên OM là trung trực của AB
=>OM vuông góc AB tại H
=>MH*MO=MA^2
Xét ΔMAC và ΔMDA có
góc MAC=góc MDA
góc AMC chung
=>ΔMAC đồng dạng với ΔMDA
=>MA/MD=MC/MA
=>MA^2=MD*MC=MH*MO

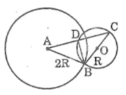
Ta có: R < OA < 3R ⇔ 2R – R < OA < 2R + R
Suy ra hai đường tròn (O ; R) và (A ; 2R) cắt nhau