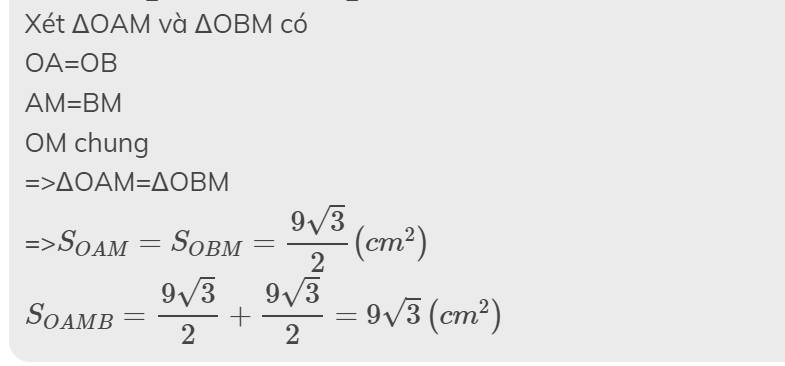Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét (O) có
MA,MB là tiếp tuyến
=>MA=MB
Xét ΔMAB có MA=MB và góc AMB=60 độ
nên ΔMAB đều
=>MA=MB=AB=18/3=6cm
Xét (O) có
MA,MB là tiếp tuyến
=>MO là phân giác của góc AMB
=>góc AMO=góc BMO=60/2=30 độ
Xét ΔOAM vuông tại A có sin AOM=OA/OM
=>OA/6=sin30=1/2
=>OA=3(cm)
ΔOAM vuông tại A
=>OA^2+AM^2=OM^2
=>\(MA=\sqrt{6^2-3^2}=3\sqrt{3}\left(cm\right)\)
\(S_{OAM}=\dfrac{1}{2}\cdot3\cdot3\sqrt{3}=\dfrac{9\sqrt{3}}{2}\left(cm^2\right)\)
Xét ΔOAM và ΔOBM có
OA=OB
AM=BM
OM chung
=>ΔOAM=ΔOBM
=>\(S_{OAM}=S_{OBM}=\dfrac{9\sqrt{3}}{2}\left(cm^2\right)\)
\(S_{OAMB}=\dfrac{9\sqrt{3}}{2}+\dfrac{9\sqrt{3}}{2}=9\sqrt{3}\left(cm^2\right)\)

Bạn tự vẽ hình được không? Rồi mình giúp, vì mình không biết sử dụng phần mềm vẽ hình.
a) Ta có: MA, MB là tiếp tuyến
=> \(OA\perp MA,OB\perp MB\)
=> \(\widehat{OBM}+\widehat{OAM}=90^o+90^o=180^o\)
=> Tứ giác OBMA nội tiếp
b) Xét tam giác MCA và MAD có
góc CMA=góc AMD
góc MDA=MAC
=> tam giác MCA đồng dạng AMD
=> \(\frac{MA}{MC}=\frac{AD}{MA}\Rightarrow MA^2=MD.MC\)
c) Gọi J là trung điểm OM
Ta có: tam giác OAM vuông tại A=> JA=JO=JM
tam giác OBM vuông tại B => JB=JM=JO
=> JA=JB=JO=JM=R
=> J là tâm đường tròn ngoại tiếp OAMN có bán kính R
I là trung điểm CD
=> OI vuông CD
=> Tam giác OIM vuông tại I có J là trung điểm OM
=> JO=JI=JM=R
=> I thuộc đường tròn ngoại tiếp tứ giác OAMN