Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hùng NguyễnPhạm Lan HươngNguyễn Lê Phước ThịnhMai.T.LoanHồng PhúcAkai Haruma

ta có góc MBO =90
góc MCO=90
MBO+MCO=90+90=180
Vậy tứ giác MBOC nội tiếp
Xét \(\Delta\)MBK và \(\Delta\) MNB
M chung
MBK=BNK(cùng chắn cung BK)
do đó\(\Delta\) MBK\(\sim\) \(\Delta\)MNB
\(\frac{MB}{MN}\)=\(\frac{MK}{MB}\) ⇒MB2=MN.MK

c. Gọi DK là đường cao của \(\Delta DPQ\)\(\left(K\in PQ\right)\)
F là giao điểm của DK với (O)\(\left(F\ne D\right)\)
Ta có: \(\widehat{OCA}=\widehat{OKA}=90^0\)
\(\Rightarrow\)Tứ giác OCAK nội tiếp.
\(\Rightarrow\widehat{COK}+\widehat{CAK}=180^0\)
Mà \(\widehat{COK}+\widehat{COF}=180^0\)
\(\Rightarrow\widehat{CAK}=\widehat{COF}\)
\(\Rightarrow\widehat{CAK}=180^0-\left(\widehat{FCO}+\widehat{CFO}\right)=180^0-2\widehat{FCO}\)(Vì \(\Delta OFC\) cân tại O (OC=OF))
Ta có: \(\widehat{FCD}=90^0\)(góc nội tiếp chắn nửa đường tròn)
\(\Rightarrow\widehat{FCO}+\widehat{OCD}=90^0\)
Lại có:\(\widehat{OCA}=\widehat{OCD}+\widehat{ACD}=90^0\)(tính chất tiếp tuyến)
\(\Rightarrow\widehat{FCO}=\widehat{ACD}\)
\(\Delta CAQ\) có: \(\widehat{CAQ}+\widehat{ACD}+\widehat{AQC}=180^0\)
\(\Rightarrow180^0-2\widehat{FCO}+\widehat{FCO}+\widehat{AQC}=180^0\)
\(\Leftrightarrow\widehat{AQC}=\widehat{FCO}=\widehat{ACQ}\)
\(\Rightarrow\Delta CAQ\)cân tại A.
Lại có: AC=AB (Tính chất tiếp tuyến)
AB=AP(\(\Delta ABP\) cân tại A)
\(\Rightarrow AP=AC=AB=AQ\)
\(\Delta CPQ\)có: \(A\in PQ;AP=AC=AQ\)
\(\Rightarrow\Delta CPQ\)vuông tại C.
=>F,C,P thẳng hàng.
=> PC là đường cao của \(\Delta DPQ\)(\(C\in DQ\))
=> F là trực tâm của \(\Delta DPQ\)
=> F trùng với H.
Mà F thuộc (O)
=> H thuộc (O)

3: góc MHO=góc MAO=góc MBO=90 độ
=>M,A,O,H,B cùng nằm trên đường tròn đường kính OM
=>góc HAB=góc HMB
CE//MB
=>góc HCE=góc HMB=góc HAB
=>ACEH nội tiếp
=>góc CHE=góc CAE
mà góc CAE=góc CDB
nên gó CHE=góc CDB
=>HE//DB
Gọi K là giao của CE và DB
Xét ΔCKD có
H là trung điểm của CD
HE//KD
=>E là trung điểm của CK
=>EC=EK
Vì CK//MB
nên CE/MF=DE/DF=EK/FB
mà CE=EK
nên MF=FB
=>F là trung điểm của MB
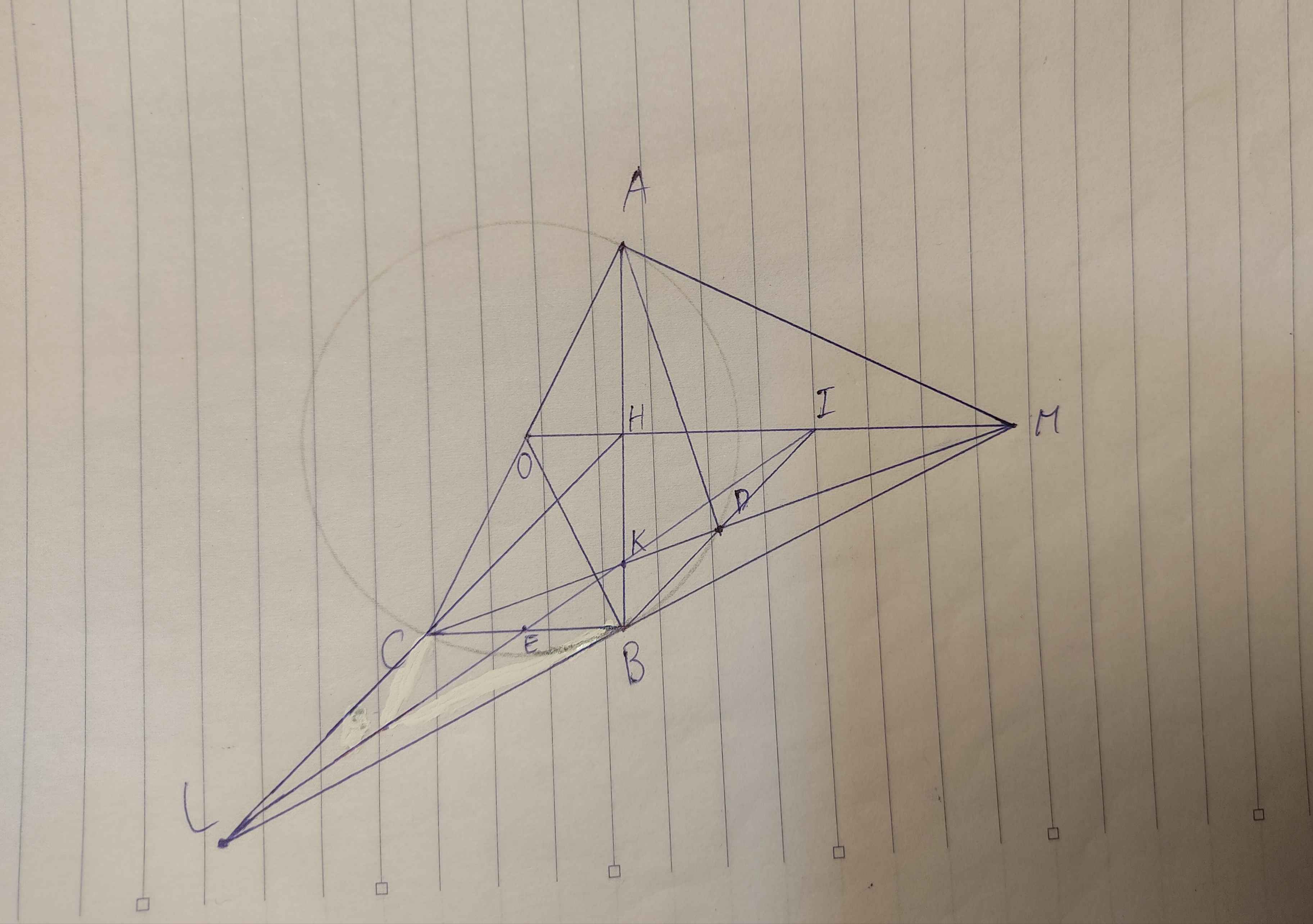

Cho mình hỏi câu B ý 2 làm sao thế