Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b: Xét (O) có
ΔCAB nội tiếp
CB là đường kính
Do đó: ΔCAB vuông tại A
=>CA\(\perp\)AB tại A
=>CA\(\perp\)BE tại A
Ta có: \(\widehat{OAE}=\widehat{OAC}+\widehat{EAC}=\widehat{OAC}+90^0\)
\(\widehat{MAC}=\widehat{MAO}+\widehat{OAC}=\widehat{OAC}+90^0\)
Do đó: \(\widehat{OAE}=\widehat{MAC}\)
Xét tứ giác CKAE có \(\widehat{CKE}=\widehat{CAE}=90^0\)
nên CKAE là tứ giác nội tiếp
=>\(\widehat{ACK}=\widehat{AEK}\)
=>\(\widehat{ACM}=\widehat{AEO}\)
Xét ΔAMC và ΔAOE có
\(\widehat{ACM}=\widehat{AEO}\)
\(\widehat{MAC}=\widehat{OAE}\)
Do đó: ΔAMC đồng dạng với ΔAOE
=>\(\dfrac{AM}{AO}=\dfrac{AC}{AE}\)
=>\(AM\cdot AE=AO\cdot AC\)


a: Ta có: ΔOAM vuông tại A
=>\(OA^2+AM^2=OM^2\)
=>\(MA^2=15^2-9^2=144\)
=>\(MA=\sqrt{144}=12\left(cm\right)\)
Xét ΔOAM vuông tại A có \(sinAMO=\dfrac{AO}{OM}=\dfrac{3}{5}\)
nên \(\widehat{AMO}\simeq36^052'\)
Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MO là phân giác của góc AMB
=>\(\widehat{AMB}=2\cdot\widehat{AMO}\simeq73^044'\)
c: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của AB
=>MO\(\perp\)AB tại H
Xét ΔOAM vuông tại A có AH là đường cao
nên \(OH\cdot OM=OA^2\)
=>\(OH\cdot OM=OC^2\)
Xét ΔOHE vuông tại H và ΔOKM vuông tại K có
\(\widehat{HOE}\) chung
Do đó: ΔOHE đồng dạng với ΔOKM
=>\(\dfrac{OH}{OK}=\dfrac{OE}{OM}\)
=>\(OK\cdot OE=OH\cdot OM\)
=>\(OK\cdot OE=OC^2\)
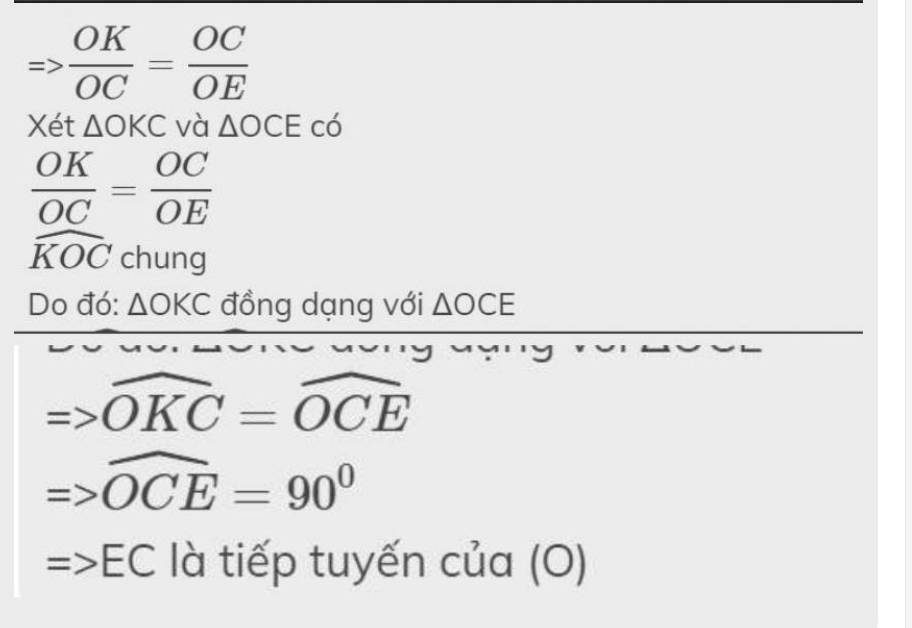
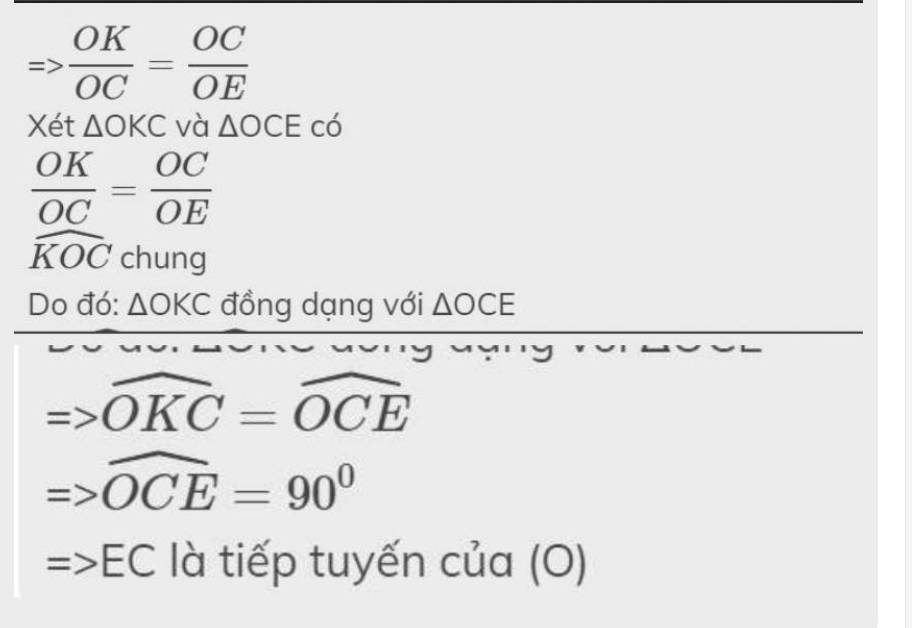
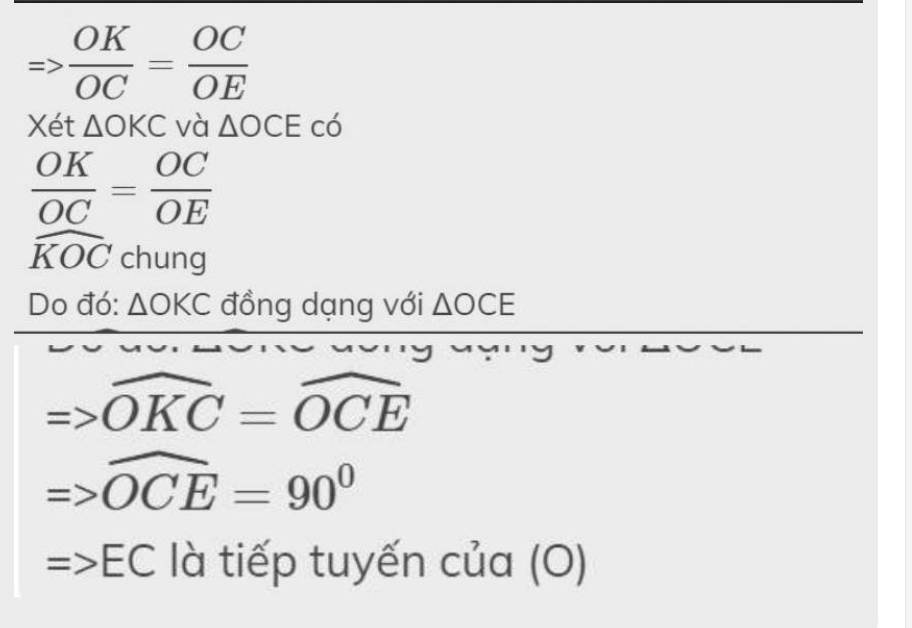
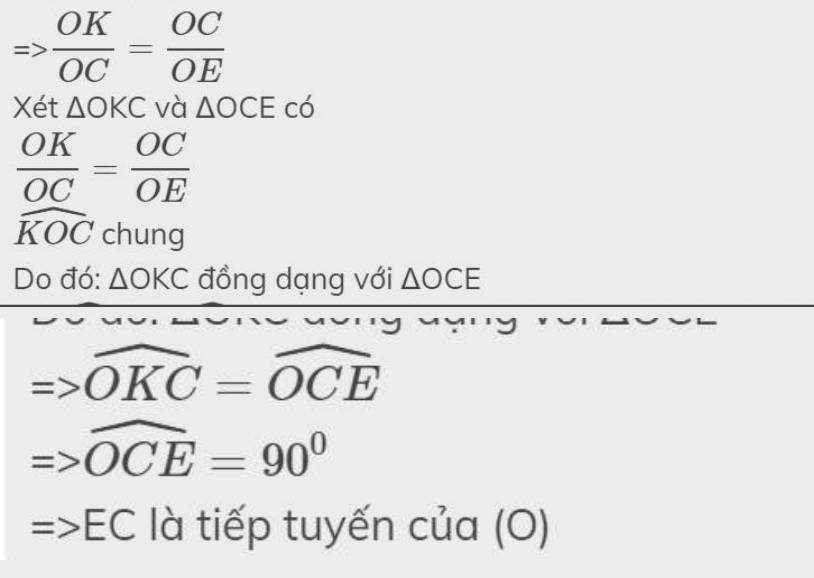
=>\(\dfrac{OK}{OC}=\dfrac{OC}{OE}\)
Xét ΔOKC và ΔOCE có
\(\dfrac{OK}{OC}=\dfrac{OC}{OE}\)
\(\widehat{KOC}\) chung
Do đó: ΔOKC đồng dạng với ΔOCE
=>\(\widehat{OKC}=\widehat{OCE}\)
=>\(\widehat{OCE}=90^0\)
=>EC là tiếp tuyến của (O)

Giải thích các bước giải:
MO là t.p.g. của AMBˆAMB^
⇒AMOˆ=BMOˆ=AMBˆ2=450⇒AMO^=BMO^=AMB^2=450
⇒ΔAMO−và−ΔBMO⇒ΔAMO−và−ΔBMO vuông cân
=> OA = AM = MB = BO
=> OAMB là h.thoi có AMBˆ=900AMB^=900
=> OAMB là h.v.
b)
PMPQ=MP+MQ+PQPMPQ=MP+MQ+PQ
=(MP+PC)+(MQ+QC)=(MP+PC)+(MQ+QC)
=(MP+PA)+(MQ+QB)=(MP+PA)+(MQ+QB)
=MA+MB=MA+MB
=2OA=2OA
=2R=2R
c)
OP−là−t.p.g.−của−AOCˆOP−là−t.p.g.−của−AOC^
⇒COPˆ=12AOCˆ⇒COP^=12AOC^ (1)
OQ−là−t.p.g.−của−BOCˆOQ−là−t.p.g.−của−BOC^
⇒COQˆ=12BOCˆ⇒COQ^=12BOC^ (2)
Cộng theo vế của (1) và (2), ta có:
COPˆ+COQˆ=12(AOCˆ+BOCˆ)=12AOBˆCOP^+COQ^=12(AOC^+BOC^)=12AOB^
⇒POQˆ=450
Giải thích các bước giải:
MO là t.p.g. của AMBˆAMB^
⇒AMOˆ=BMOˆ=AMBˆ2=450⇒AMO^=BMO^=AMB^2=450
⇒ΔAMO−và−ΔBMO⇒ΔAMO−và−ΔBMO vuông cân
=> OA = AM = MB = BO
=> OAMB là h.thoi có AMBˆ=900AMB^=900
=> OAMB là h.v.
b)
PMPQ=MP+MQ+PQPMPQ=MP+MQ+PQ
=(MP+PC)+(MQ+QC)=(MP+PC)+(MQ+QC)
=(MP+PA)+(MQ+QB)=(MP+PA)+(MQ+QB)
=MA+MB=MA+MB
=2OA=2OA
=2R=2R
c)
OP−là−t.p.g.−của−AOCˆOP−là−t.p.g.−của−AOC^
⇒COPˆ=12AOCˆ⇒COP^=12AOC^ (1)
OQ−là−t.p.g.−của−BOCˆOQ−là−t.p.g.−của−BOC^
⇒COQˆ=12BOCˆ⇒COQ^=12BOC^ (2)
Cộng theo vế của (1) và (2), ta có:
COPˆ+COQˆ=12(AOCˆ+BOCˆ)=12AOBˆCOP^+COQ^=12(AOC^+BOC^)=12AOB^
⇒POQˆ=450vv

Câu hỏi của Mafia - Toán lớp 9 - Học toán với OnlineMath
Em có thể tham khảo tại đây nhé.