Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

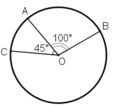

* Trường hợp 1 . Điểm C nằm trên cung lớn AB.
Do điểm C nằm trên cung lớn AB nên tia OA nằm giữa hai tia OB và OC.
Do 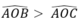 nên tia OA nằm giữa hai tia OB và OC hay A nằm trên cung BC.
nên tia OA nằm giữa hai tia OB và OC hay A nằm trên cung BC.
Suy ra: 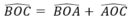 = 1000+ 450 = 1450
= 1000+ 450 = 1450
Khi đó, số đo cung nhỏ BC là 1450 ( bằng góc ở tâm 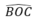 )
)
Số đo cung lớn BC là: 3600 - 1450 = 2150
* Trường hợp 2: Điểm C nằm trên cung nhỏ AB
Vì điểm C nằm trên cung nhỏ AB nên OC nằm giữa OA và OB
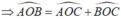
Ta có: 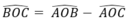 = 1000- 450 = 550
= 1000- 450 = 550
Khi đó, số đo cung nhỏ BC là 550
Số đo cung lớn BC là: 3600- 550 = 3050

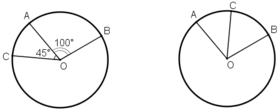
* Trường hợp 1 . Điểm C nằm trên cung lớn AB.
Do điểm C nằm trên cung lớn AB nên tia OA nằm giữa hai tia OB và OC.
Do ![]() nên tia OA nằm giữa hai tia OB và OC hay A nằm trên cung BC.
nên tia OA nằm giữa hai tia OB và OC hay A nằm trên cung BC.
Suy ra: ![]() =
100
0
+
45
0
=
145
0
=
100
0
+
45
0
=
145
0
Khi đó, số đo cung nhỏ BC là
145
°
( bằng góc ở tâm 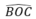 )
)
Số đo cung lớn BC là: 360 0 − 145 0 = 215 0
* Trường hợp 2: Điểm C nằm trên cung nhỏ AB
Vì điểm C nằm trên cung nhỏ AB nên OC nằm giữa OA và OB
![]()
Ta có: ![]() =
100
0
−
45
0
=
55
0
=
100
0
−
45
0
=
55
0
Khi đó, số đo cung nhỏ BC là 55 0
Số đo cung lớn BC là: 360 0 − 55 0 = 305 0
Kiến thức áp dụng
+ Góc có đỉnh trùng với tâm đường tròn được gọi là góc ở tâm.
+ Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
+ Số đo của cung lớn bằng hiệu của 360º và số đo của cung nhỏ (có chung hai mút với cung lớn).

a/
\(sđ\widehat{ACO}=\dfrac{1}{2}\left(sđcungAD-sđcungBE\right)\) (góc có đỉnh ngoài hình tròn)
\(\Rightarrow sđ\widehat{ACO}=\dfrac{1}{2}sđcungAD-\dfrac{1}{2}sđcungBE\) (1)
Ta có
\(sđ\widehat{AOD}=sđcungAD\) (Góc có đỉnh là tâm đường tròn)
\(\Rightarrow\dfrac{1}{2}sđcungAD=\dfrac{1}{2}sđ\widehat{AOD}\) (2)
Ta có
BC = OB = R => tg BOC cân tại B \(\Rightarrow\widehat{ACO}=\widehat{BOE}\) (góc ở đáy tg cân)
\(sđ\widehat{BOE}=sđcungBE\) (Góc có đỉnh là tâm đường tròn)
\(\Rightarrow\dfrac{1}{2}sđ\widehat{ACO}=\dfrac{1}{2}sđ\widehat{BOE}=\dfrac{1}{2}sđcungBE\) (3)
Thay (2) và (3) vào (1)
\(\Rightarrow sđ\widehat{ACO}=\dfrac{1}{2}sđ\widehat{AOD}-\dfrac{1}{2}sđ\widehat{ACO}\)
\(\Rightarrow2.sđ\widehat{ACO}=sđ\widehat{AOD}-sđ\widehat{ACO}\)
\(\Rightarrow sđ\widehat{AOD}=3.sđ\widehat{ACO}\)
b/
Ta có
AB = R = OA = OB => tg OAB là tg đều
\(\Rightarrow\widehat{OAB}=\widehat{OBA}=60^o\)
\(\Rightarrow\widehat{OBC}=180^o-\widehat{OBA}=180^o-60^o=120^o\)
Xét tg cân BOC có
\(\widehat{BCO}+\widehat{BOC}=180^o-\widehat{OBC}=180^o-120^o=60^o\)
Mà \(\widehat{BCO}=\widehat{BOC}\) (góc ở đáy tg cân)
\(\Rightarrow\widehat{BCO}=\widehat{BOC}=30^o\)
Xét tg AOC có
\(\widehat{AOC}=180^o-\left(\widehat{OAB}+\widehat{BOC}\right)=180^o-\left(60^o+30^o\right)=90^o\)
=> tg AOC vuông tại O
AC = AB + BC = 2R
\(\Rightarrow CO=\sqrt{AC^2-OA^2}=\sqrt{4R^2-R^2}=R\sqrt{3}\)

a: Xet ΔOAC có OA=OC và OA^2+OC^2=AC^2
nên ΔOAC vuôg cân tại O
b: \(BC=\sqrt{AB^2-AC^2}=\sqrt{4R^2-2R^2}=R\sqrt{2}\)
c: ΔOAC vuông cân tại O
=>góc BAC=45 độ
+) Có A,B thuộc đường tròn (O;R)
=> OA = OB = R Mà AB = R
=> OA = OB = AB => tam giác AOB đều ( định nghĩa tam giác đều)
=> góc AOB = 60 độ ( tính chất tam giác đều)
Trong đường tròn (O;R) có góc AOB là góc ở tâm chắn cung AB nhỏ
=> số đo cung AB nhỏ = góc AOB = 60 độ (tính chất góc ở tâm )
+) Có B,C thuộc đường tròn (O;R) => OB=OC=R
Có OB^2 + OC^2 = R^2 + R^2= 2*R^2 = BC^2 ( vì BC = R\(\sqrt{2}\) )
=> tam giác BOC vuông ở O ( định lý Py-ta-go đảo )
=> góc BOC = 90 độ
Trong đường tròn (O;R) có góc BOC là góc ở tâm chắn cung BC nhỏ
=> góc BOC = số đo cung BC nhỏ ( tính chất góc ở tâm) => số đo cung BC nhỏ = 90 độ
+) Vì tia BO nằm giữa 2 tia BA và BC nên B nằm giữa A và C
=> số đo cung AB nhỏ + số đo cung BC nhỏ = số đo cung AC nhỏ
=> số đo cung AC nhỏ = 60 độ + 90 độ = 150 độ
k cho mk nha !!!!!!!!!!!