Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

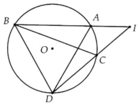
a, HS tự chứng minh
b, ∆IAC:∆IDB (g.g)
c, Sử dụng kết quả câu b)

2: góc BEA=1/2*180=90 độ
Xét ΔBMN vuông tại M và ΔBEA vuông tại E có
góc MBN chung
=>ΔBMN đồng dạng với ΔBEA
=>BM/BE=BN/BA
=>BE*BN=BA*BM=BC^2
=>AC^2+BE*BN=AB^2=4*R^2

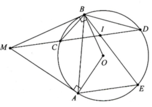
a, Vì M B C ^ = M D B ^ = 1 2 s đ C B ⏜ nên chứng minh được ∆MBC:∆MDB (g.g)
b, Vì
M
B
O
^
+
M
A
O
^
=
180
0
nên tứ giác MAOB nội tiếp
c, Đường tròn đường kính OM là đường tròn ngoại tiếp tứ giác MAOB => r = M O 2
Gọi H là giao điểm của AB với OM
=> OH ⊥ AB; AH = BH = R 3 2
Giải tam giác vuông OAM, đường cao AH ta được OM = 2R Þ r = R
d, Ta có M I B ^ = s đ D E ⏜ + s đ B C ⏜ 2 và M A B ^ = s đ A C ⏜ + s đ B C ⏜ 2
Vì AE song song CD => s đ D E ⏜ = s đ A C ⏜ => M I B ^ = M A B ^
Do tứ giác MAIB nội tiếp hay 5 điểm A, B, O, I, M nằm trên cùng 1 đường tròn kính MO
Từ đó ta có được M I O ^ = 90 0 => OI ⊥ CD hay I là trung điểm của CD

a,Xét tứ giác ACHI có: góc ACB = 90o (góc nội tiếp chắn nửa đường tròn)
góc HIA = 90o (gt)
=> tổng hai góc này =180o mà đỉnh C và I lại nằm ở vị trí đối nhau => tứ giác ACHI là tứ giác nội tiếp đường tròn đường kính AH (đpcm)




a) So sánh \(\widehat{ACI}\) và \(\widehat{ABD}\) và cặp góc \(\widehat{CAI}\) và \(\widehat{CDB}\)
Ta có \(\widehat{ACI}+\widehat{ACD}=180^o\) (hai góc kề bù) \(\left(1\right)\)
Xét \(\left(O\right)\) có:
\(\widehat{ABD}\) là góc nối tiếp chắn cung \(AD\)
\(\widehat{ACD}\) là góc nối tiếp chắn cung \(AD\)
\(\Rightarrow\widehat{ABD}+\widehat{ACD}=\dfrac{1}{2}.360^o=180^o\) \(\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) ⇔ \(\widehat{ACI}=\widehat{ABD}=180^o-\widehat{ACD}\)
Ta có: \(\widehat{CAI}+\widehat{BAC}=180^o\) (hai góc kề bù)
Xét \(\left(O\right)\) có:
\(\widehat{BAC}\) là góc nội tiếp của chắn cung \(BC\)
\(\widehat{CDB}\) là góc nội tiếp của chắn cung \(BC\)
\(\Rightarrow\widehat{BAC}+\widehat{CDB}=\dfrac{1}{2}.360^o=180^o\) \(\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) \(\Rightarrow\widehat{CAI}=\widehat{CDB}=180^o-\widehat{BAC}\)
b) Chứng minh tam giác IAC đồng dạng với tam giác IDB
Xét \(\Delta IAC\) và \(\Delta IDB\) có:
\(\widehat{A}\) là góc chung
\(\widehat{IAC}=\widehat{IDB}\) (câu a)
\(\Rightarrow\Delta IAC\sim\Delta IDB\)
c) Chứng minh \(IA.IB=IC.ID\)
Theo câu b ta có \(\Delta IAC\sim\Delta IDB\)
Suy ra: \(\dfrac{IA}{ID}=\dfrac{IC}{IB}\)
Hay: \(IA.IB=IC.ID\) (đpcm)
a: ACDB là tứ giác nội tiếp
=>góc ABD+góc ACD=180 độ;góc BAC+góc BDC=180 độ
=>góc ACI=góc ABD;góc CAI=góc CDB
b: Xét ΔIAC và ΔIDB có
góc IAC=góc IDB
góc AIC chung
=>ΔIAC đồng dạg với ΔIDB
c: ΔIAC đồng dạng vơi ΔIDB
=>IA/ID=IC/IB
=>IA*IB=IC*ID