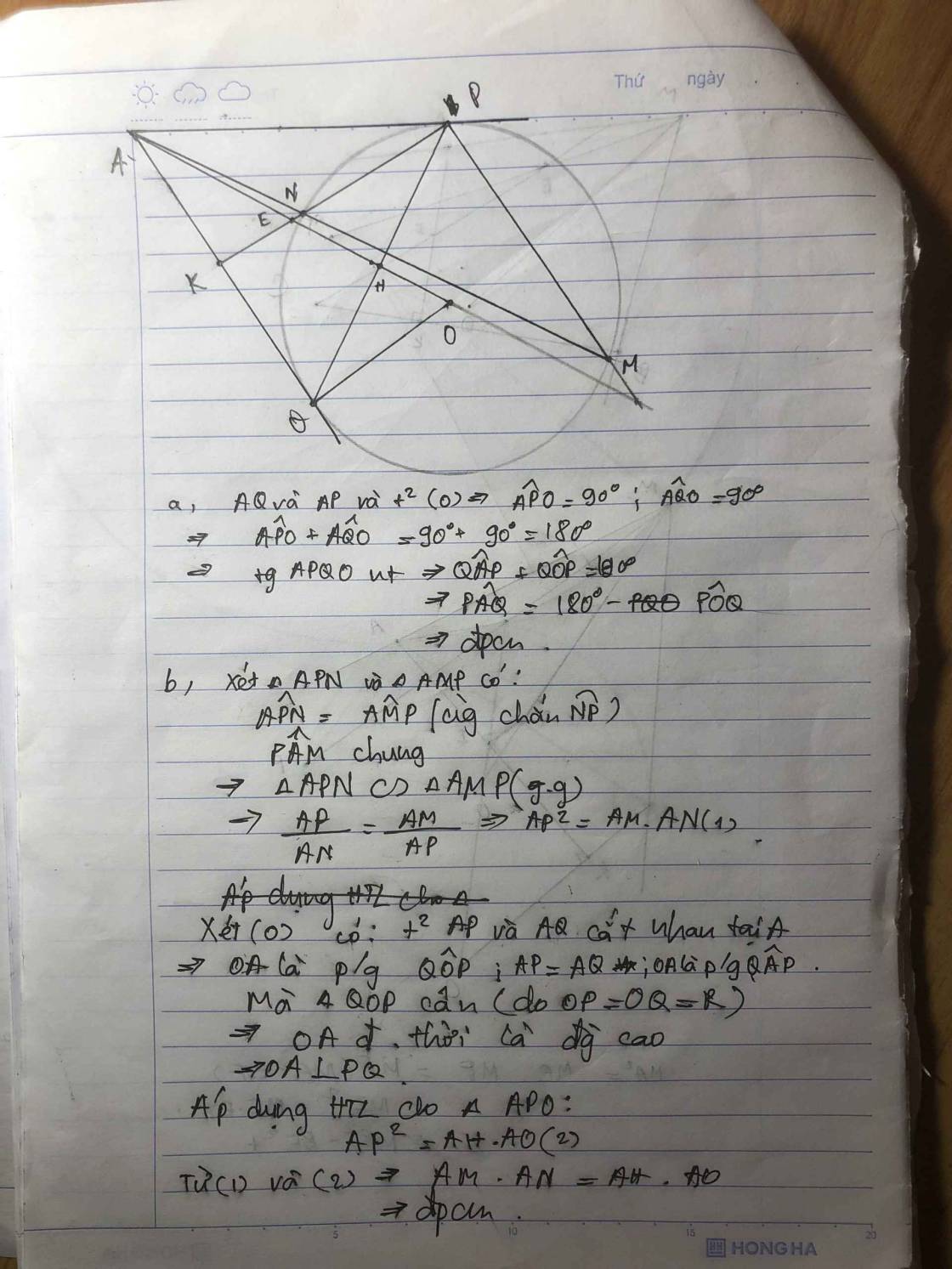Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có ABAB và ACAC là tiếp tuyến tại AA và BB của (O)(O)
⇒AB⊥OB⇒AB⊥OB và AC⊥OCAC⊥OC
Xét AOB và ΔAOCAOB và ΔAOC có:
OB=OC(=R)OB=OC(=R)
ˆABO=ˆACO=90oABO^=ACO^=90o
OAOA chung
⇒ΔAOB=ΔAOC⇒ΔAOB=ΔAOC (ch-cgv)
⇒AB=AC⇒AB=AC và có thêm OB=OC⇒AOOB=OC⇒AO là đường trung trực của BCBC
Mà H là trung điểm của BC
⇒A,H,O⇒A,H,O thẳng hàng
Tứ giác ABOCABOC có ˆABO+ˆACO=90o+90o=180oABO^+ACO^=90o+90o=180o
⇒A,B,C,O⇒A,B,C,O cùng thuộc đường tròn đường kính OAOA.

Tóm tắt thôi nhé
a) Các cạnh // => Hình bình hành
T/g OBE = t/g OCD (^B=^C=90*, OB=OC, ^BOE=^COD vì cùng phụ với EOD) => OE = OD (2 cạnh kề) => Hình thoi
b) Nối OO' => 2 tam giác cân cùng góc đáy => so le trong => //
c) 1] OO' là đường trung trực của AB => đường trung bình
2] CB//OO'
Cm tương tự 1] để được BD//OO' => Ơ-clit => thẳng hàng

a) Ta có: \(\angle MAO=\angle MHO=90\Rightarrow MAHO\) nội tiếp
b) Xét \(\Delta MAB\) và \(\Delta MCA:\) Ta có: \(\left\{{}\begin{matrix}\angle MAB=\angle MCA\\\angle CMAchung\end{matrix}\right.\)
\(\Rightarrow\Delta MAB\sim\Delta MCA\left(g-g\right)\Rightarrow\dfrac{AB}{AC}=\dfrac{MA}{MC}\)
c) Vì MAHO nội tiếp \(\Rightarrow\angle BHA=\angle MOA\)
Ta có: \(\angle ABH=180-\angle MBA=180-\angle MAC=\angle AMO\) \((AC\parallel MO)\)
mà \(\angle MOA+\angle AMO=90\Rightarrow\angle BHA+\angle ABH=90\Rightarrow\angle BAH=90\)
d) MO cắt CD tại E
Vì \(OE\parallel AC\) mà \(AC\bot CD\left(\angle ACD=90\right)\Rightarrow OE\bot CD\)
mà \(OC=OD\Rightarrow OE\) là trung trực CD
mà \(M\in OE\Rightarrow\angle DMO=\angle CMO=\angle ACH\) \((MO\parallel AC)\)
Ta có: \(\angle DOM=180-\angle MOA=180-\angle MHA\left(MAHOnt\right)=\angle AHC\)
Xét \(\Delta AHC\) và \(\Delta DOM:\) Ta có: \(\left\{{}\begin{matrix}\angle DOM=\angle AHC\\\angle DMO=\angle ACH\end{matrix}\right.\)
\(\Rightarrow\Delta AHC\sim\Delta DOM\left(g-g\right)\)

a) Xét tứ giác ABOC: ^ABO=^ACO=900 (Do AB và AC là 2 tiếp tuyến của (O))
=> Tứ giác ABOC nội tiếp đường tròn dường kính AO (1)
Ta có: DE là dây cung của (O), I là trung điểm DE => OI vuông góc DE => ^OIA=900
Xét tứ giác ABOI: ^ABO=^OIA=900 => Tứ giác ABOI nội tiếp đường tròn đường kính AO (2)
(1) + (2) => Ngũ giác ABOIC nội tiếp đường tròn
Hay 4 điểm B;O;I;C cùng thuộc 1 đường tròn (đpcm).
b) Gọi P là chân đường vuông góc từ D kẻ đến OB
Ta có: Tứ giác BOIC nội tiếp đường tròn => ^ICB=^IOP (Góc ngoài tại đỉnh đối) (3)
Dễ thấy tứ giác DIPO nội tiếp đường tròn đường kính OD
=> ^IOP=^IDP (=^IDK) (4)
(3) + (4) => ^ICB=^IDK (đpcm).
c) ^ICB=^IDK (cmt) => ^ICH=^IDH => Tứ giác DHIC nội tiếp đường tròn
=> ^DIH=^DCH hay ^DIH=^DCB.
Lại có: ^DCB=^DEB (2 góc nội tiếp cùng chắn cung BD) => ^DIH=^DEB
Mà 2 góc trên đồng vị => IH // EB hay IH // EK
Xét tam giác KDE: I là trung điểm DE (Dễ c/m); IH // EK; H thuộc DK
=> H là trung điểm DK (đpcm).

a: Xét tứ giác ABOC có
\(\widehat{OBA}+\widehat{OCA}=180^0\)
=>OBAC là tứ giác nội tiếp
b: Xét (O) có
DB,DM là tiếp tuyến
=>DB=DM và OD là phân giác của \(\widehat{BOM}\left(1\right)\)
Xét (O) có
EM,EC là tiếp tuyến
=>EM=EC và OE là phân giác của \(\widehat{MOC}\left(2\right)\)
\(C_{ADE}=AD+DE+AE\)
\(=AB-BD+DM+ME+AC-CE\)
\(=AB+AC=2AB\)
c: \(\widehat{DOE}=\widehat{DOM}+\widehat{EOM}\)
\(=\dfrac{1}{2}\left(\widehat{BOM}+\widehat{COM}\right)=\dfrac{1}{2}\cdot\widehat{BOC}\)