Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
1.
Vì $MA, MB$ là tiếp tuyến của $(O)$ nên:
$MA\perp OA, MB\perp OB$
$\Rightarrow \widehat{MAO}=\widehat{MBO}=90^0$
Tứ giác $MAOB$ có tổng 2 góc đối nhau $\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0$ nên là tứ giác nội tiếp.
$\Rightarrow M, A, O,B$ cùng thuộc 1 đường tròn.
2.
Vì $MA=MB, OA=OB$ nên $MO$ là trung trực cuả $AB$
$\Rightarrow MO\per AB$ tại $H$
Xét tam giác $AMO$ vuông tại $A$ có đường cao $AH$. Áp dụng hệ thức lượng trong tgv thì:
$MA^2=MH.MO$
Xét tam giác $MCB$ và $MBD$ có:
$\widehat{M}$ chung
$\widehat{MBC}=\widehat{MDB}$ (góc tạo bởi tiếp tuyến và dây cung thì bằng góc nội tiếp chắn cung đó)
$\Rightarrow \triangle MCB\sim \triangle MBD$ (g.g)
$\Rightarrow \frac{MC}{MB}=\frac{MB}{MD}$
$\Rightarrow MC.MD=MB^2$
Mà $MB^2=MA^2\Rightarrow MA^2=MH.MO=MC.MD$ (đpcm)

a: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của BA(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của AB
=>MO\(\perp\)AB tại trung điểm H của AB
b: Xét (O) có
\(\widehat{MAP}\) là góc tạo bởi tiếp tuyến AM và dây cung AP
\(\widehat{AQP}\) là góc nội tiếp chắn cung AP
Do đó: \(\widehat{MAP}=\widehat{AQP}\)
=>\(\widehat{MAP}=\widehat{MQA}\)
Xét ΔMAP và ΔMQA có
\(\widehat{MAP}=\widehat{MQA}\)
\(\widehat{AMP}\) chung
Do đó: ΔMAP đồng dạng với ΔMQA
=>\(\dfrac{MA}{MQ}=\dfrac{AP}{QA}\left(1\right)\)
Xét (O) có
ΔQAP nội tiếp
QP là đường kính
Do đó: ΔQAP vuông tại A
Xét ΔHAP vuông tại H và ΔHQA vuông tại H có
\(\widehat{HAP}=\widehat{HQA}\left(=90^0-\widehat{HPA}\right)\)
Do đó: ΔHAP đồng dạng với ΔHQA
=>\(\dfrac{HA}{HQ}=\dfrac{AP}{QA}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{MA}{MQ}=\dfrac{HA}{HQ}\)
=>\(MA\cdot HQ=MQ\cdot HA\)


a, Chú ý: A M O ^ = A I O ^ = A N O ^ = 90 0
b, A M B ^ = M C B ^ = 1 2 s đ M B ⏜
=> DAMB ~ DACM (g.g)
=> Đpcm
c, AMIN nội tiếp => A M N ^ = A I N ^
BE//AM => A M N ^ = B E N ^
=> B E N ^ = A I N ^ => Tứ giác BEIN nội tiếp => B I E ^ = B N M ^
Chứng minh được: B I E ^ = B C M ^ => IE//CM
d, G là trọng tâm DMBC Þ G Î MI
Gọi K là trung điểm AO Þ MK = IK = 1 2 AO
Từ G kẻ GG'//IK (G' Î MK)
=> G G ' I K = M G M I = M G ' M K = 2 3 I K = 1 3 A O không đổi (1)
MG' = 2 3 MK => G' cố định (2). Từ (1) và (2) có G thuộc (G'; 1 3 AO)

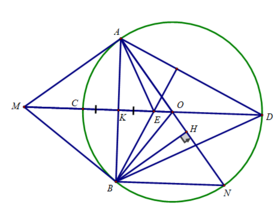
d) Ta có:
K là trung điểm của CE (E đối xứng với C qua AB)
K là trung điểm của AB
AB ⊥ CE (MO ⊥ AB)
⇒ Tứ giác AEBC là hình thoi
⇒ BE // AC
Mà AC ⊥ AD (A thuộc đường tròn đường kính CD)
Nên BE ⊥ AD và DK ⊥ AB
Vậy E là trực tâm của tam giác ADB