Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(ABC\) cân tại A \(\Rightarrow\widehat{ABC}=\widehat{ACB}\)
\(\left\{{}\begin{matrix}\widehat{ACB}+\widehat{BCH}=90^0\\\widehat{CBH}+\widehat{BCH}=90^0\end{matrix}\right.\) \(\Rightarrow\widehat{ACB}=\widehat{CBH}\)
\(\Rightarrow\widehat{ABC}=\widehat{CBH}\)
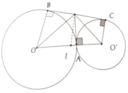
a, Chứng minh được tương tự câu 1a,
=> O ' M O ^ = 90 0
Áp dụng hệ thức lượng trong tam giác vuông tính được MA = R r
b, Chứng minh
S
B
C
O
O
'
=
R
+
r
R
r
c, Chứng minh được: ∆BAC:∆OMO’ => S B A C S O M O ' = B C O O ' 2
=> S B A C = S O M O ' . B C 2 O O ' 2 = 4 R r R r R + r
d, Tứ giác OBCO’ là hình thang vuông tại B và C có IM là đường trung bình => IM ⊥ BC = {M}
a.Xét 2 tam giác vuông ABO và ACO có
BO=CO (đều là BK đường tròn)
AB=AC (Độ dài hai tiếp tuyến của một đường tròn cùng xuất phát từ một điểm bên ngoài đường tròn thì bằng nhau)
góc ABO=góc ACO=90 độ
Suy ra tam giác ABO=tam giác ACo (c.g.c) suy ra góc BAO=góc CAO
Tam giác ABC cân tại A nên AO vừa là phân giác của góc BAC vừa là đường cao của tam giác ABC hạ từ A xuống BC vậy AO vuông góc với BC
c,Ta có góc BCO=góc CAO (cùng phụ với góc AOC)
góc CAO=góc BAO
suy ra góc BCO=góc BAO (1)
Xét tam giác vuông BCH có góc CBH+góc BCO=90 độ (2)
Ta có góc ABC+góc BAO=90 độ (3)
Từ (1) (2) (3) suy ra góc CBH=góc ABC nên BC là phân giác của góc ABH
mình chỉ biết làm câu a và c thôi mong bạn thông cảm
Chọn đáp án C.
Ta có:
Góc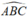
là góc tạo bởi tia tiếp tuyến và dây cung chắn cung BC⌢ nên: