Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

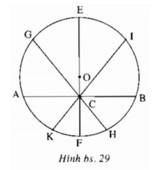
Dây lớn nhất đi qua C là đường kính EF = 50cm. Dây nhỏ nhất đi qua C là dây AB vuông góc với OC tại C, AB = 48 cm.
Có tất cả 4 dây đi qua C có độ dài là một số nguyên xentimet.

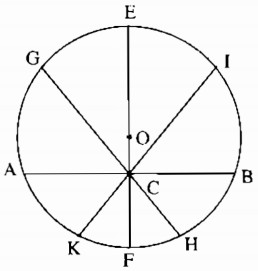
Dây lớn nhất đi qua C là đường kính EF = 50cm.
Dây nhỏ nhất đi qua C là dây AB vuông góc với OC tại C .
- Áp dụng định lý pi ta go vào tam giác OAC vuông tại C có : \(AC=\sqrt{OA^2-OC^2}=\sqrt{25^2-7^2}=24\left(cm\right)\)
Có hai dây đi qua C có độ dài 49cm là dây GH và IK đối xứng nhau qua EF .
Vậy có tất cả 4 dây đi qua C có độ dài là một số nguyên xentimét.

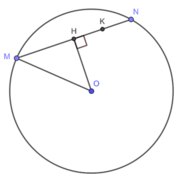
Ta có tam giác MON cân tại O
Mà ∠ OMN = 45 ° suy ra, tam giác OMN vuông cân tại O
OH là đường cao của tam giác MON
Suy ra, OH là đường trung tuyến của tam giác MON
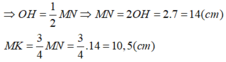
Đáp án: A

Dây lớn nhất đi qua C là đường kính EF = 50cm
Dây nhỏ nhất đi qua C là dây AB vuông góc với OC tại C, AB = 48cm.
Có hai dây đi qua C có độ dài 49cm(dây GH và IK đối xứng qua EF)
Có tất cả 4 dây đi qua C có độ dài là 1 số nguyên cm.