Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác ABOC có
\(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
=>ABOC là tứ giác nội tiếp
=>A,B,O,C cùng thuộc một đường tròn
b: Xét (O) có
AB,AC là tiếp tuyến
Do đó: AB=AC và AO là phân giác của góc BAC
Ta có: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
từ (1) và (2) suy ra AO là đường trung trực của BC
=>OA\(\perp\)BC
c: Xét ΔOBA vuông tại B có \(sinBAO=\dfrac{OB}{OA}=\dfrac{1}{2}\)
nên \(\widehat{BAO}=30^0\)
Ta có: AO là phân giác của góc BAC
=>\(\widehat{BAC}=2\cdot\widehat{BAO}=60^0\)
Ta có: ΔOBA vuông tại B
=>\(BO^2+BA^2=OA^2\)
=>\(BA^2=\left(2R\right)^2-R^2=3R^2\)
=>\(BA=R\sqrt{3}\)
Xét ΔBAC có AB=AC và \(\widehat{BAC}=60^0\)
nên ΔBAC đều
=>\(S_{BAC}=\dfrac{BA^2\cdot\sqrt{3}}{4}=\dfrac{3R^2\cdot\sqrt{3}}{4}\)

a, 700 góc nào bạn ?
b, Vì AB là tiếp tuyến (O) => ^ABO = 900
AO giao BC = K
AB = AC ; OB = OC = R
Vậy OA là đường trung trực đoạn BC
Xét tam giác ABO vuông tại B, đường cao BK
Áp dụng định lí Pytago tam giác ABO vuông tại B
\(AB=\sqrt{AO^2-BO^2}=\sqrt{16-4}=2\sqrt{3}\)cm
Áp dụng hệ thức : \(BK.AO=BO.AB\Rightarrow BK=\frac{BO.AB}{AO}=\frac{4\sqrt{3}}{4}=\sqrt{3}\)cm
Vì AO là đường trung trực => \(BC=2KB=2\sqrt{3}\)cm
Chu vi tam giác ABC là :
\(P_{ABC}=AB+AC+BC=2AB+BC=4\sqrt{3}+2\sqrt{3}=6\sqrt{3}\)cm

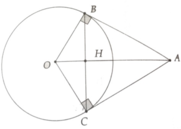
a, HS tự làm
b,i, Áp dụng định lý Pytago tính được BH = 3 cm
Áp dụng hệ thức lược về cạnh góc vuông và đường cao trong tam giác vuông, tính được:
AB = AC = 2 3 cm => P A B C = 6 3 cm, S A B C = 3 3 c m 2
ii, Ta có: S A B O C = S A B C + S B O C = 4 3 c m 2

a: BA là tiếp tuyến của (O) có B là tiếp điểm
=>OB\(\perp\)BA tại B
=>ΔOBA vuông tại B
ΔBOA vuông tại B
=>\(BO^2+BA^2=OA^2\)
=>\(BA^2=\left(2R\right)^2-R^2=3R^2\)
=>\(BA=R\sqrt{3}\)
b: ΔOBC cân tại O
mà OA là đường cao
nên OA là tia phân giác của \(\widehat{BOC}\)
Xét ΔOBA và ΔOCA có
OB=OC
\(\widehat{BOA}=\widehat{COA}\)
OA chung
Do đó: ΔOBA=ΔOCA
=>\(\widehat{OCA}=\widehat{OBA}=90^0\)
=>AC là tiếp tuyến của (O)
c: Xét ΔABO vuông tại B có \(sinBAO=\dfrac{BO}{OA}=\dfrac{1}{2}\)
nên \(\widehat{BAO}=30^0\)
ΔOBA=ΔOCA
=>\(\widehat{BAO}=\widehat{CAO}\) và AB=AC
=>\(\widehat{BAC}=2\cdot\widehat{BAO}=2\cdot30^0=60^0\)
Xét ΔABC có AB=AC và \(\widehat{BAC}=60^0\)
nên ΔABC đều

Đáp án B
* Theo tính chất hai tiếp tuyến cắt nhau ta có:
AB = AC; DB = DM; EM = EC
suy ra: DE = DM + ME = DB + EC.
* Chu vi tam giác ADE là:
AD + AE + DE = AD + AE + DB + EC
= (AD + DB ) + ( AE + EC ) = AB + AC = 2AB ( vì AB = AC )

a: Xét ΔOBA và ΔOCA có
OB=OC
\(\widehat{BOA}=\widehat{COA}\)
OA chung
Do đó: ΔOBA=ΔOCA
Suy ra: \(\widehat{OBA}=\widehat{OCA}\)
hay AC là tiếp tuyến của (O)
Chu vi tam giác ABC bằng 4 3 cm