Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
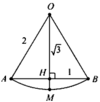
Gọi H, M lần lượt là giao điểm của d với AB và dây cung A B ⏜
Tam giác O A B đều cạnh 2 ⇒ O H = O A 3 2 = 3 ⇒ H M = 2 − 3
Quay tam giác O A B quanh trục d ta được khối nón N có bán kính đáy r = A H = 1 và chiều cao h = O H = 3
⇒ Thể tích khối nón N là V N = 1 3 π r 2 h = 3 3 π
Quay phần hình còn lại quanh trục d ta được chỏm cầu C có bán kính đáy r = A H = 1 và chiều cao h = H M = 2 − 3
⇒ Thể tích khối nón C là V C = π h 6 3 r 2 + h 2 = 16 − 9 3 3 π
Vậy thể tích khối tròn xoay (H) là
V = V N + V C = 16 − 8 3 3 π ≈ 2 , 24
Đáp án B
Giari thích các bước :
Gọi H, M lần lượt là giao điểm của d với AB và dây cung A B ⏜
Tam giác O A B đều cạnh 2 ⇒ O H = O A 3 2 = 3 ⇒ H M = 2 − 3
Quay tam giác O A B quanh trục d ta được khối nón N có bán kính đáy r = A H = 1 và chiều cao h = O H = 3
⇒ Thể tích khối nón N là V N = 1 3 π r 2 h = 3 3 π
Quay phần hình còn lại quanh trục d ta được chỏm cầu C có bán kính đáy r = A H = 1 và chiều cao h = H M = 2 − 3
⇒ Thể tích khối nón C là V C = π h 6 3 r 2 + h 2 = 16 − 9 3 3 π
Vậy thể tích khối tròn xoay (H) là
V = V N + V C = 16 − 8 3 3 π ≈ 2 , 24

Đáp án D.
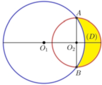
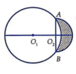
Gắn hệ trục tọa độ Oxy sao cho O 1 ≡ O (gốc tọa độ).
Phương trình đường tròn O 1 ; 5 là x 2 + y 2 = 5 2 ⇒ y = ± 25 − x 2 .
Tam giác O 1 O 2 A vuông tại O 2 , có O 1 O 2 = O 1 A 2 − O 2 A 2 = 5 2 − 3 2 = 4.
Phương trình đường tròn O 2 ; 3 là x − 4 2 + y 2 = 9 ⇒ y = ± 9 − x − 4 2 .
Gọi V 1 là thể tích của khối tròn xoay sinh ra khi quay hình phẳng D 1 được giới hạn bởi các đường y = 9 − x − 4 2 , y = 0 , x = 4 , x = 7 quanh trục tung ⇒ V 1 = π ∫ 4 7 9 − x − 4 2 d x .
Gọi V 2 là thể tích của khối tròn xoay sinh ra khi quay hình phẳng D 2 được giới hạn bởi các đường y = 25 − x 2 , y = 0 , x = 4 , x = 5 quanh trục tung ⇒ V 2 = π ∫ 4 5 25 − x 2 d x .
Khi đó, thể tích cần tính là:
V = V 1 − V 2 = π ∫ 4 7 9 − x − 4 2 d x − π ∫ 4 5 25 − x 2 d x = 40 π 3 .

Đáp án C

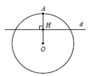
Chọn hệ tọa độ Oxy như hình vẽ với O 3 ≡ O , O 2 C ≡ O x , O 2 A ≡ O y .
Ta có
O 1 O 2 = O 1 A 2 − O 2 A 2 = 5 2 − 3 2 = 4 ⇒ O 1 − 4 ; 0 .
Phương trình đường tròn O 1 : x + 4 2 + y 2 = 25.
Phương trình đường tròn O 2 : x 2 + y 2 = 9.
Kí hiệu H 1 là hình phẳng giới hạn bởi các đường O 2 : x 2 + y 2 = 9, trục Oy: x = 0 khi x ≥ 0 .
Kí hiệu H 2 là hình phẳng giới hạn bởi các đường O 2 : x 2 + y 2 = 9, trục Oy: x=0 khi x ≥ 0 .
Khi đó thể tích V cần tìm chíình bằng thể tích V 2 của khối tròn xoay thu được khi quay hình H 2 xung quanh trục Ox (thể tích nửa khối cầu bán kính bằng 3) trừ đi thể tích V 1 của khối tròn xoay thu được khi quay hình H 1 xung quanh trục Ox.
Ta có V 2 = 1 2 . 4 3 π 3 3 = 18 π (đvtt);
V 1 = π ∫ 0 1 y 2 d x = π ∫ 0 1 25 − x + 4 2 d x = 14 π 3 (đvtt).
Vậy V = V 2 − V 1 = 18 π − 14 π 3 = 40 π 3 (đvtt).


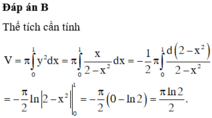
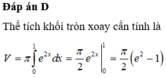




Đáp án A
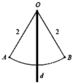
Khi quay hình tròn C quay trục OA ta được khối cầu có thể tích V = 4 3 π R 3 = 36 π
Khối tròn xoay H 1 chưa điểm A chính là chỏm cầu có chiều cao x 2 + 4
Suy ra thể tích khối H 1 là V 1 = π h 2 R − h 3 = π . A H 2 . 3 − A H 3
Mà V = V 1 + V 2 và
V 2 = 2 V 1 ⇒ V 1 V = 1 3 = A H 2 . 3 − A H 3 36 = 1 3 ⇔ A H 3 − 9 A H 2 + 36 = 0 *
Vì 0 < A H < O A = 3 nên giải * → c a s i o A H ≈ 2 , 32