Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
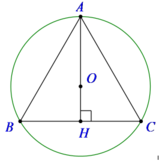
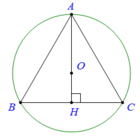
AH là đường cao trong tam giác đều cạnh a nên A H = a 3 2
Gọi O là tâm mặt cầu ngoại tiếp ΔABC, thì O ∈ AH và
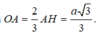
Bán kính mặt cầu được tạo thành khi quay đường tròn (C) quanh trục AH là 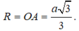 .
.
Vậy thể tích của khối cầu tương ứng là:
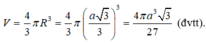

Chọn C
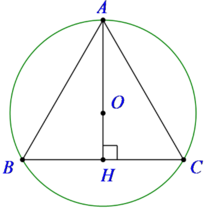
AH là đường cao trong tam giác đều cạnh a nên A H = a 3 2
Gọi O là tâm mặt cầu ngoại tiếp ΔABC, thì O ∈ AH và 
Bán kính mặt cầu được tạo thành khi quay đường tròn (C) quanh trục AH là 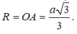
Vậy thể tích của khối cầu tương ứng là:
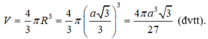

Chọn D.
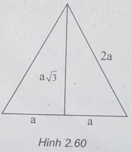
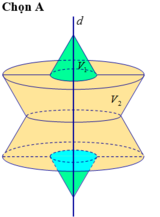
(h.2.60) Bán kính đáy của hình nón là a, đường sinh của hình nón là 2a.
Do đó, ta có:
S 1 = π Rl = π .a.2a = 2 πa 2 (1)
Mặt cầu có bán kính là a 3 /2, nên ta có:
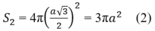
Từ (1) và (2) suy ra: 2 S 2 = 3 S 1

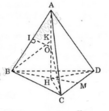
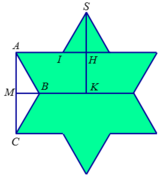
a,+) Từ A vẽ AH _|_ (BCD) (theo giả thiết AB = AC = AD)
Nên \(\Delta ABH=\Delta ACH=\Delta ADH\)
=> HB = HC = HD
Vậy H là tâm đường tròn ngoại tiếp tam giác BCD
+) Ta có: \(AH=\sqrt{AB^2-BH^2}\) với \(BH=\dfrac{2}{3}BM=\dfrac{2}{3}\cdot\dfrac{a\sqrt{3}}{3}\)
\(\Rightarrow AH=\sqrt{a^2-\dfrac{3a^2}{9}}=\dfrac{a\sqrt{6}}{3}\)
b, Ta có: \(H=AH=\dfrac{a\sqrt{6}}{3};r=BH=\dfrac{a\sqrt{3}}{3}\)
Diện tích xung quanh hình trụ là:
\(S_{xq}=2\pi rh=2\pi.\dfrac{a\sqrt{3}}{3}.\dfrac{a\sqrt{6}}{3}=\dfrac{2\pi\pi^2\sqrt{2}}{3}\)
Thể tích khối trụ là:
\(V=\pi r^2h=\pi\left(\dfrac{a\sqrt{3}}{3}\right)^2.\dfrac{a\sqrt{6}}{3}=\dfrac{\pi a^3\sqrt{6}}{9}\)

![]()
Diện tích xung quanh của hình trụ là:
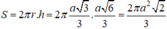
Thể tích của khối trụ là;
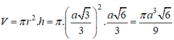

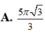
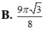
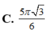
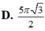
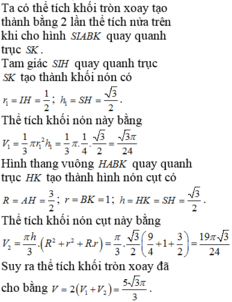
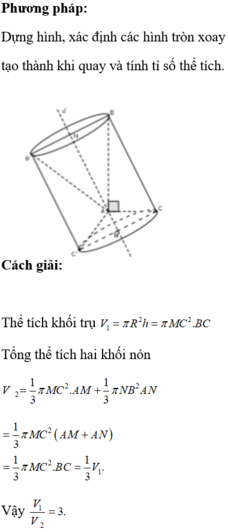
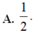
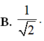
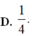
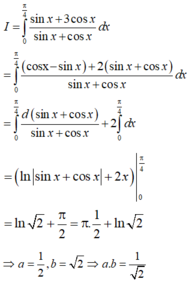
Đáp án C
Bán kính mặt cầu được tạo thành khi quay đường tròn (C) quanh trục AH là