Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
Phương pháp: Tính độ dài đoạn thẳng IM với I là tâm mặt cầu.
Tham số hóa tọa độ điểm M, sau đó dựa vào độ dài IM để tìm điểm M.
Cách giải : Mặt cầu (S) có tâm I(1;2; – 3) bán kính R = 3 3
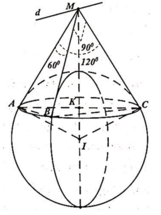
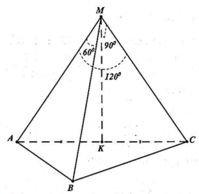
Đặt MA = MB = MC = a
Tam giác MAB đều => AB = a
Tam giác MBC vuông tại M => BC = a 2
Tam giác MCA có C M A ^ = 120 0 => AC = a 3
Xét tam giác ABC có A B 2 + B C 2 = A C 2 => ∆ABC vuông tại B
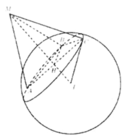
=>∆ABC ngoại tiếp đường tròn nhỏ có đường kính AC
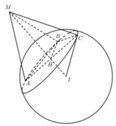
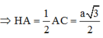
Xét tam giác vuông IAM có:
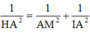
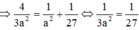
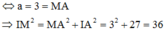
![]()
![]()
![]()
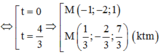
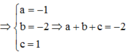

Gọi I(x;y;z) là điểm thỏa mãn 3 I A ⇀ - 2 I B ⇀ = 0 → ⇔ 3 I A ⇀ = 2 I B ⇀
Ta có ![]()
![]()
Khi đó 3 I A ⇀ = 2 I B ⇀
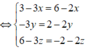
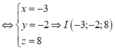
Ta có:
![]()
![]()
(vì 3 I A ⇀ - 2 I B ⇀ = 0 ⇀ )
Khi đó | 3 M A ⇀ - 2 M B ⇀ | = | M I ⇀ | = M I nhỏ nhất khi M là hình chiếu của I trên mặt phẳng (P)
Phương trình đường thẳng d qua I(-3;-2;8) và vuông góc với (P) là

Suy ra M = d ∩ ( P ) nên tọa độ điểm M là nghiệm của hệ
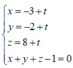
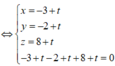

Từ đó ![]()
⇒ S = 9 a + 3 b + 6 c = - 33 - 8 + 44 = 3
Chọn đáp án B.

Đáp án D
Phương pháp:
+ Tìm tâm và bán kính của mặt cầu
+ Xác định vị trí tương đối của mặt phẳng và mặt cầu để suy ra vị trí của điểm M
+ Tìm tọa độ của đường thẳng và mặt cầu thì ta giải hệ phương trình gồm phương trình đường thẳng và phương trình mặt cầu
Cách giải:
Mặt cầu (S) có tâm
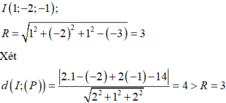
nên mặt phẳng (P) không cắt mặt cầu (S).Khi đó điểm M thuộc mặt cầu (S) sao cho khoảng cách từ M đến mặt phẳng (P) là nhỏ nhất thì M là giao điểm của đường thẳng d đi qua I , nhận n P → = 2 ; - 1 ; 2 làm VTCP với mặt cầu.
Phương trình đường thẳng
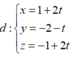
Tọa độ giao điểm của đường thẳng d và mặt cầu (S) thỏa mãn hệ phương trình
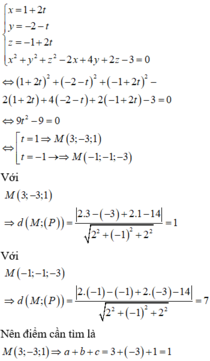

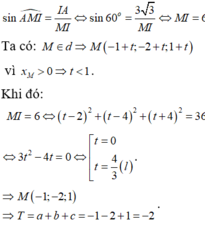

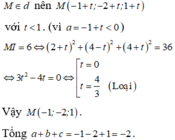

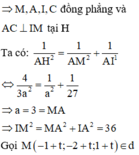
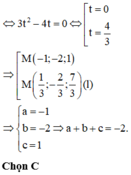



Phương pháp:
Đưa phương trình đường thẳng d về dạng tham số t, biểu diễn tọa độ điểm M theo tham số t.
Tính MA + 2MB + 3MC theo tham số t rồi lập luận để biểu thức đạt giá trị nhỏ nhất.