Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Gọi A’ là điểm đối xứng với A qua d
- Nối A’B cắt d tại M . M chính là điểm cần tìm .
- Thật vậy : \(\left|MA-MB\right|=\left|MA'-MB\right|=A'B\)
. Giả sử tồn tại một điểm M’ khác với M trên d , khi đó : \(\left|M'A-M'B\right|=\left|M'A'-M'B\right|\le A'B\)
Dấu bằng chỉ xảy ra khi M’A’B thẳng hàng, nghĩa là M trùng với M’.

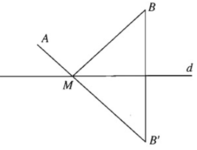
Gọi B' là ảnh của B qua phép đối xứng qua trục d.
Khi đó với mỗi điểm M thuộc d
MA + MB = MA + MB′ nên MA + MB′ bé nhất
⇔ A, M, B′ thẳng hàng.
Tức là M = (AB′) ∩ d.

Gọi `M(x;3/2x+5/2)`
Ta có:`|\vec{MA}-2\vec{MB}|`
`=|(4-x;7-3/2x-5/2)-2(2-x;1-3/2x-5/2)|`
`=|(x;3/2x+17/2)|`
`=\sqrt{x^2+(3/2x+17/2)^2}`
`=\sqrt{x^2+9/4x^2+51/2x+289/4}`
`=\sqrt{13/4x^2+51/2x+289/4}`
`=\sqrt{(\sqrt{13}/2 x+[51\sqrt{13}]/26)^2+289/13} >= [17\sqrt{13}]/13`
Dấu "`=`" xảy ra `<=>\sqrt{13}/2x+[51\sqrt{13}]/26=0<=>x=-51/13`
`=>M(-51/13;-44/13)`

Cách 1:
Do M thuộc d, gọi tọa độ M có dạng \(M\left(2m-2;m\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\left(2m-2;m-6\right)\\\overrightarrow{BM}=\left(2m-4;m-5\right)\end{matrix}\right.\)
Đặt \(T=MA+MB=\sqrt{\left(2m-2\right)^2+\left(m-6\right)^2}+\sqrt{\left(2m-4\right)^2+\left(m-5\right)^2}\)
\(T=\sqrt{5m^2-20m+40}+\sqrt{5m^2-26m+41}\)
\(T=\sqrt{5\left(m-2\right)^2+\left(2\sqrt{5}\right)^2}+\sqrt{5\left(\dfrac{13}{5}-m\right)^2+\left(\dfrac{6}{\sqrt{5}}\right)^2}\)
\(T\ge\sqrt{5\left(m-2+\dfrac{13}{5}-m\right)^2+\left(2\sqrt{5}+\dfrac{6}{\sqrt{5}}\right)^2}=\sqrt{53}\)
Dấu "=" xảy ra khi và chỉ khi:
\(6\left(m-2\right)=10\left(\dfrac{13}{5}-m\right)\Leftrightarrow m=\dfrac{19}{8}\)
\(\Rightarrow M\left(\dfrac{11}{4};\dfrac{19}{8}\right)\)
Cách 2:
Thay tọa độ A và B vào pt (d) được 2 giá trị cùng dấu âm \(\Rightarrow A;B\) nằm cùng phía so với (d)
Gọi d' là đường thẳng qua A và vuông góc với d \(\Rightarrow\) pt d' có dạng:
\(2\left(x-0\right)+1\left(y-6\right)=0\Leftrightarrow2x+y-6=0\)
Gọi C là giao điểm của d và d' \(\Rightarrow\left\{{}\begin{matrix}x-2y+2=0\\2x+y-6=0\end{matrix}\right.\)
\(\Rightarrow C\left(2;2\right)\)
Gọi D là điểm đối xứng với A qua d \(\Leftrightarrow C\) là trung điểm AD \(\Rightarrow D\left(4;-2\right)\)
Phương trình BD có dạng: \(7\left(x-2\right)+2\left(y-5\right)=0\Leftrightarrow7x+2y-24=0\)
\(MA+MB\) nhỏ nhất khi và chỉ khi M là giao điểm của BD
\(\Rightarrow\) Tọa độ M thỏa mãn: \(\left\{{}\begin{matrix}7x+2y-24=0\\x-2y+2=0\end{matrix}\right.\) \(\Rightarrow M\left(\dfrac{11}{4};\dfrac{19}{8}\right)\)

\(T=\left(x_A-2y_A+2\right)\left(x_B-2y_B+2\right)=60>0\)
=> A và B nằm cùng phía so với d
a)Lấy B' đối xứng với B qua d
=> d là trung trực của BB'
Có \(MA+MB=MA+MB'\)
Để MA+MB nn <=> MA+MB' nhỏ nhất <=> M;A;B' thẳng hàng <=> \(\overrightarrow{AM};\overrightarrow{AB'}\) cùng phương
\(BB'\left\{{}\begin{matrix}quaB\left(2;5\right)\\\perp d\Rightarrow vtcp\overrightarrow{n}\left(2;1\right)\end{matrix}\right.\)
\(\Rightarrow BB':2x+y-9=0\)
Gọi \(F=BB'\cap d\) \(\Rightarrow F\left(\dfrac{16}{5};\dfrac{13}{5}\right)\)
F là trung điểm của BB' \(\Rightarrow B'\left(\dfrac{22}{5};\dfrac{1}{5}\right)\)
\(M\in\left(d\right)\Rightarrow M\left(2t-2;t\right)\)
\(\Rightarrow\overrightarrow{AB'}\left(\dfrac{22}{5};-\dfrac{29}{5}\right)\);\(\overrightarrow{AM}\left(2t-2;t-6\right)\)
\(\overrightarrow{AM};\overrightarrow{AB'}\) cp <=> \(\dfrac{22}{5}\left(t-6\right)=-\dfrac{29}{5}\left(2t-2\right)\)
<=>\(t=\dfrac{19}{8}\)
Vậy \(M\left(\dfrac{11}{4};\dfrac{19}{8}\right)\)
b) Có \(MA-MB\le AB\)
\(\Leftrightarrow\left|MA-MB\right|\le AB\)
\(\left|MA-MB\right|\) lớn nhất <=> M;A;B thẳng hàng <=> \(\overrightarrow{AM};\overrightarrow{AB}\) cp
\(M\in\left(2t-2;t\right)\)
\(\Rightarrow\overrightarrow{AM}\left(2t-2;t-6\right)\); \(\overrightarrow{AB}\left(2;-1\right)\)
\(\overrightarrow{AM};\overrightarrow{AB}\) cp <=> \(-1\left(2t-2\right)=2\left(t-6\right)\)
\(\Leftrightarrow t=\dfrac{7}{2}\)
\(\Rightarrow\) \(M\left(5;\dfrac{7}{2}\right)\)

Lấy A’’ đối xứng với A qua d.
Chu vi tam giác ABC = AB + AC + BC = AB + CA’’+ CB
Vì độ dài AB không đổi nên để chu vi tam giác ABC nhỏ nhất khi và chỉ khi CA” + CB nhỏ nhất.
Lại có; C A " + C B ≥ A " B
Do đó, để chu vi tam giác ABC nhỏ nhất khi và chỉ khi CA” + CB = A”B. Khi đó: B, C, A’’ thẳng hàng.
Đáp án C

Lấy A' đối xứng với A qua d. Khi đó: AM+MB=A'M+MB>=A'B.
Vậy (AM+MB)min <=> A', M, B thẳng hàng.
Cách dựng: Lấy A' đối xứng A qua d, A'B cắt d tại M. M là điểm cần tìm

- Tìm điểm A’ đối xứng với A qua d
- Nối A’B cắt d tại M. M chính là điểm cần tìm.
- Thật vậy : Vì A’ đối xứng với A qua d cho nên MA=MA’. Do đó : MA+MB=MA’+MB=A’B .
- Giả sử tồn tại M’ khác M thuộc d thì : M’A+M’B=M’A’+M’B lớn hơn hoặc bằng A'B. Dấu bằng chỉ xảy ra khi A’M’B thẳng hàng. Nghĩa là M trùng với M’
Làm sao tìm được điểm đối xứng vậy bạn? Mình không hiểu rõ (trong mặt phẳng tọa độ nhà)