Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tạo thành 2 góc trong cùng phía bù nhau.
=> a //b
=> a) b) c) đúng

Tham khao
a) Hình vẽ:
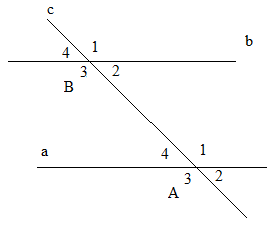
b) Ta có: ˆA4=ˆB2A4^=B2^
ˆA1+ˆA4=180∘A1^+A4^=180∘ (Hai góc kề bù)
ˆB2+ˆB3=180∘B2^+B3^=180∘ (Hai góc kề bù)
Suy ra ˆA1=ˆB3A1^=B3^
Quảng cáo
c) ˆA4=ˆB2A4^=B2^
ˆA2=ˆA4A2^=A4^ (Hai góc đối đỉnh)
Suy ra: ˆA2=ˆB2A2^=B2^
Các cặp góc đồng vị khác tương tự.
d) ˆA4=ˆB2A4^=B2^
ˆA1+ˆA4=180∘A1^+A4^=180∘ (Hai góc kề bù)
Suy ra ˆA1+ˆB2=180∘A1^+B2^=180∘
e) ˆA2=ˆB2A2^=B2^ (theo câu c)
ˆB2+ˆB1=180∘B2^+B1^=180∘ (Hai góc kề bù)
Suy ra ˆA1+ˆB2=180∘

a)
c cắt a,b tại A, B
Mà \(a//b\) \(\text{a // b và \widehat{A_4} + \widehat{B_1} =180^O (1)}\)và \(\widehat{A_4}+\widehat{B_1}=180^O\left(1\right)\)
Ta có: \(\widehat{A_4}+\widehat{B_3}=180^O\left(2\right)\)
\(\widehat{B}_1+\widehat{B}_2=180^O\left(3\right)\)
Từ (1) , (2) ,(3) \(\Rightarrow\)\(\widehat{A}_3=\widehat{B}_1\)
Từ (1) và (3)\(\Rightarrow\widehat{A}_4=\widehat{B}_2\)
Do đó các cặp so le không bằng nhau
b)
\(\widehat{A}_1=\widehat{A_3}\left(đđ\right)\)
\(\widehat{A}_4=\widehat{A}_2\left(//\right)\)
\(\Rightarrow\widehat{A}_1=\widehat{B}_1\left(=\widehat{A}_3\right)\)
\(\widehat{A_2}=\widehat{B}_2\left(=\widehat{A}_4\right)\)
\(\widehat{B}_1=\widehat{B}_3,\widehat{B}_2=\widehat{B}_4\left(dđ\right)\)
\(\Rightarrow\widehat{A}_4=\widehat{B}_4\left(=\widehat{B}_2\right),\widehat{A}_3=\widehat{B}_3\left(=\widehat{B_1}\right)\)
Do đó hai góc đồng vị bằng nhau
c)
\(\widehat{A}_3=\widehat{B}_1,\widehat{B}_2=\widehat{A}_4\)
\(\Rightarrow\widehat{A}_3+\widehat{B}_2=\widehat{B}_1+\widehat{A}_4=180^O\)
Cặp góc không cùng phía còn lại bù nhau
#Shinobu Cừu

Nếu một đường thẳng cắt hai đường thẳng song song thì:
A. Hai góc so le trong bù nhau
B. Hai góc trong cùng phía bằng nhau
C. Hai góc đồng vị bằng nhau
D. Hai góc trong cùng phía bù nhau
đáp án là:
C. Hai góc đồng vị bằng nhau
D. Hai góc trong cùng phía bù nhau

a) Ta có các cặp góc đồng vị là: A1 và B1; A2 và B2 ; A3 và B3 ; A4 và B4
Giả sử đã cho : A1 = B1
ta có: A1 = A3 (đối đỉnh) ; B1 = B3 (đối đỉnh) => A3 =B3
Ta có: A1 + A2 = 180o (2 góc kề bù)
B1 + B2 = 180o (2 góc kề bù)
Mà A1 = B1 nên A2 = B2
Tương tự, A2 = A4 và B2 = B4 (đối đỉnh) nên A4 = B4
b) Các cặp góc so le trong là: A2 và B4 ; A3 và B1
Theo câu a) A2 = B2 mà B2 = B4 (do đối đỉnh) nên A2 = B4
Tương tư với A3 và B1
c) các cặp góc so le ngoài là: A1 và B3 ; A4 và B2
Ta có: A1 = B1 ( giả thiết) mà B1 = B3 (do đối đỉnh) => A1 = B3
A4 và B2 : tương tự
d) Các cặp góc trong cùng phía: A2 và B1 ; A3 và B4
Ta có: A1 + A2 = 180o (do kề bù)
Mà A1 = B1 nên B1 + A2 = 180o => A2 và B1 bù nhau
A3 và B4 : tương tự
e) các cặp góc ngoài cùng phía : A1 và B2 ; A4 và B3
Ta có: B1 + B2 = 180o ( do kề bù)
Mà A1 = B1 nên A1 + B2 = 180o => A1 và B2 bù nhau
A4 và B3 : tương tự

Đường thẳng c cắt hai đường thẳng a,b tương ứng tại A,B
\(\widehat{A}_1=\widehat{B}_3\) \((1)\)
a, Cặp góc so le trong còn lại là : \(\widehat{A}_4\) và \(\widehat{B}_2\)
\(\widehat{A}_4=180^0-\widehat{A_1}\) \((2)\)
\(\widehat{B}_2=180^0-\widehat{B}_3\) \((3)\)
Từ 1,2,3 suy ra \(\widehat{A}_4=\widehat{B}_2\) \((4)\)
b, Xét một cặp góc đồng vị , chẳng hạn \(\widehat{A}_3\)và \(\widehat{B}_3\)
\(\widehat{A}_3=\widehat{A}_1\) hai góc đối đỉnh \((5)\)
Kết hợp với 1 suy ra :
\(\widehat{A}_3=\widehat{B}_3\) \((6)\)
Xét tương tự cho các cặp góc đồng vị khác
P/S : Hoq chắc :<