Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

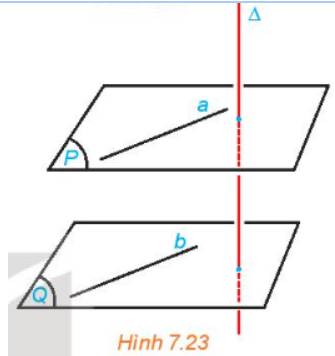
\(\left. \begin{array}{l}\Delta \bot \left( P \right)\\a \subset \left( P \right)\end{array} \right\} \Rightarrow \Delta \bot a,a//b \Rightarrow \Delta \bot b \Rightarrow \left( {\Delta ,b} \right) = {90^0}\)
\(\Delta \bot a \Rightarrow \left( {\Delta ,a} \right) = {90^0}\)
\( \Rightarrow \) (\(\Delta \), b) = (\(\Delta \), a) mà b là đường thẳng bất kì thuộc (Q)
\( \Rightarrow \) \(\Delta \bot \left( Q \right)\)

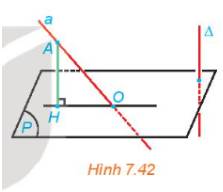
+) AH // \(\Delta \) (cùng vuông góc (P))
\( \Rightarrow \) (a, \(\Delta \)) = (a, AH) = \(\widehat {HAO}\)
+) HO là hình chiếu của a trên (P)
\( \Rightarrow \) (a, (P)) = (a, HO) = \(\widehat {AOH}\)
Mà tam giác AHO vuông tại H \( \Rightarrow \) \(\widehat {HAO}\) và \(\widehat {AOH}\) phụ nhau.
\( \Rightarrow \) Góc giữa a và (P) có mối quan hệ với góc giữa a và \(\Delta \) là 2 góc phụ nhau.

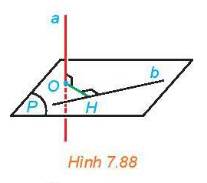
\(a\perp\left(P\right)\) tại O
\(OH\subset\left(P\right)\)
Do đó: \(a\perp OH\)
mà \(b\perp OH\)
nên \(d\left(a;b\right)=OH\)

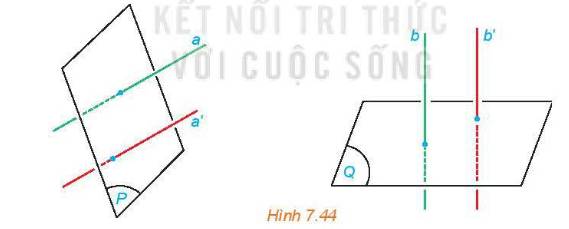
Vì hai đường thẳng a, a' cùng vuông góc với (P), hai đường thẳng b, b' cùng vuông góc với (Q) nên a // a', b // b'
Vậy (a,b) = (a', b')

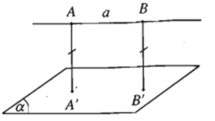
Lấy điểm A ∈ a, A’ là hình chiếu của A trên mặt phẳng (α) ⇒ AA’ = khoảng cách từ A đến mặt phẳng (α)
Mà khoảng cách từ A đến mặt phẳng (α) là bé nhất so với các khoảng cách từ A tới một điểm bất kì của mặt phẳng (α).
Vậy khoảng cách giữa đường thẳng a và mặt phẳng (α) là bé nhất so với khoảng cách từ một điểm bất kì thuộc a tới một điểm bất kì thuộc mặt phẳng (α).

a) Ta có:
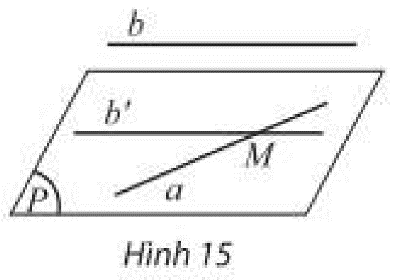
\(\left. \begin{array}{l}b\parallel b'\\b' \subset \left( P \right)\end{array} \right\} \Rightarrow b\parallel \left( P \right)\)
b) Theo hệ quả 1, ta có:
\(\left. \begin{array}{l}b\parallel \left( {P'} \right)\\M \in b'\\b\parallel b'\end{array} \right\} \Rightarrow b' \subset \left( {P'} \right)\)
\(\begin{array}{l}\left. \begin{array}{l}a \subset \left( P \right)\\a \subset \left( {P'} \right)\end{array} \right\} \Rightarrow a = \left( P \right) \cap \left( {P'} \right)\\\left. \begin{array}{l}b' \subset \left( P \right)\\b' \subset \left( {P'} \right)\end{array} \right\} \Rightarrow b' = \left( P \right) \cap \left( {P'} \right)\end{array}\)
Do đó \(a\) và \(b'\) đều là các đường thẳng chung của hai mặt phẳng \(\left( P \right)\) và \(\left( {P'} \right)\).
Vì \(a\) và \(b'\) phân biệt, mà hai mặt phẳng phân biệt chỉ có duy nhất một đường thẳng chung nên \(\left( P \right) \equiv \left( {P'} \right)\).

Lấy M thuộc a
=>\(M\in\left(P\right)\)
a//(Q)
\(\Leftrightarrow d\left(a;\left(Q\right)\right)=d\left(M;\left(Q\right)\right)\)
(P)//(Q)
=>\(d\left(\left(P\right);\left(Q\right)\right)=d\left(M;\left(Q\right)\right)\)
Do đó: \(d\left(a;\left(Q\right)\right)=d\left(\left(P\right),\left(Q\right)\right)\)

tham khảo:
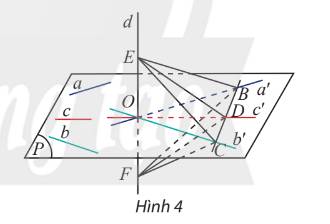
a) Vì a//a', d⊥a nên d⊥a′, Hay EF⊥OB
Tam giác EBF có OB⊥EF; O là trung điểm EF nên tam giác EBF cân tại B. Suy ra BE = BF
Tương tự ta chứng minh được CE = CF
Suy ra tam giác CEB bằng tam giác CFB
b) Vì tam giác CEB và CFB bằng nhau nên DE = DF
Nên tam giác DEF cân tại D có DO là trung tuyến nên DO⊥EF
Suy ra d⊥c
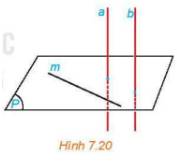
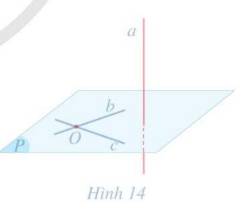

\(\left. \begin{array}{l}a \bot \left( P \right)\\m \subset \left( P \right)\end{array} \right\} \Rightarrow a \bot m \Rightarrow \left( {a,m} \right) = {90^0}\)
a // b \( \Rightarrow \left( {a,m} \right) = \left( {b,m} \right) = {90^0}\) mà đường thẳng m bất kì thuộc mặt phẳng (P)
\( \Rightarrow \) b \( \bot \) (P).