Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có nhận xét: tổng độ dài hai cạnh của hai hình vuông bằng AB là độ dài không đổi.
Từ O, M, O' hạ các đường vuông góc với AB như hình vẽ.
Ta có: OX bằng nửa cạnh hình vuông AICD; O'Y bằng nửa cạnh hình vuông BIEF.
=> OX + OY = 1/2 AB là đại lượng không đổi
MZ là đường trung bình của hình thang O'YXO
=> MZ = 1/2 (OX + OY) = 1/2 . 1/2 AB = 1/4 AB
Suy ra khoảnh cách từ M đến AB là đại lượng không đổi ( = 1/4 AB).
Vậy M nằm trên đường thẳng song song với AB và cách AB bằng độ dài bằng 1/4 AB
đáp án là M nằm trên đường thẳng song song với AB và cách AB bằng độ dài bằng 1/4 AB

Ta có nhận xét: tổng độ dài hai cạnh của hai hình vuông bằng AB là độ dài không đổi.
Từ O, M, O' hạ các đường vuông góc với AB như hình vẽ.
Ta có: OX bằng nửa cạnh hình vuông AICD; O'Y bằng nửa cạnh hình vuông BIEF.
=> OX + OY = 1/2 AB là đại lượng không đổi
MZ là đường trung bình của hình thang O'YXO
=> MZ = 1/2 (OX + OY) = 1/2 . 1/2 AB = 1/4 AB
Suy ra khoảnh cách từ M đến AB là đại lượng không đổi ( = 1/4 AB).
Vậy M nằm trên đường thẳng song song với AB và cách AB bằng độ dài bằng 1/4 AB

https://olm.vn/hoi-dap/detail/61999750098.html
Câu hỏi của Hoàng Phúc - Toán lớp 8 - Học toán với OnlineMath
Một cách của a@olm.vn

Tương tự bài 4. kéo dài AC và BD cắt nhau tại E. Từ đó chứng minh được I thuộc đường trung bình của DABE.

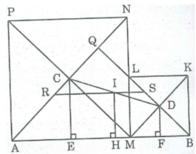
Gọi Q là giao điểm của BL và AN.
Ta có:
AN ⊥ MP (tính chất hình vuông)
BL ⊥ MK (tính chất hình vuông)
MP ⊥ MK (tính chất hình vuông)
Suy ra:
BL ⊥ AN ⇒ ∆ QAB vuông cân tại Q cố định.
M thayđổi thì I thay đổi luôn cách đoạn thẳng AB cố định một khoảng không đổi bằng a/4 nên I chuyển động trênđường thẳng song song với AB, cách AB một khoảng bằng a/4.
Khi M trùng B thì I trùng với S là trung điểm của BQ.
Khi M trùng với A thì I trùng với R là trung điểm của AQ.
Vậy khi M chuyển động trên đoạn AB thì I chuyển động trên đoạn thẳng RS song song với AB, cách AB một khoảng bằng a/4

Tương tự 2B. Gợi ý: Kéo dài AC và BD cắt nhau tại E. Xét các trường hợp khi M º A Þ C º A, D º E và khi M º B Þ D º B, C º E.
Từ đó chứng minh được I thuộc đường trung bình của DABE.
Giải
Ta có nhận xét: tổng độ dài hai cạnh của hai hình vuông bằng AB là độ dài không đổi.
Từ O, M, O' hạ các đường vuông góc với AB như hình vẽ.
Ta có: OX bằng nửa cạnh hình vuông AICD; O'Y bằng nửa cạnh hình vuông BIEF.
=> OX + OY = 1/2 AB là đại lượng không đổi
MZ là đường trung bình của hình thang O'YXO
=> MZ = 1/2 (OX + OY) = 1/2 . 1/2 AB = 1/4 AB
Suy ra khoảnh cách từ M đến AB là đại lượng không đổi ( = 1/4 AB).
Vậy M nằm trên đường thẳng song song với AB và cách AB bằng độ dài bằng 1/4 AB