Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho điểm O nằm giữa hai điểm A và B và điểm M sao cho hai tia OM và OB trùng nhau. Chứng tỏ rằng:

a) Vì điểm O nằm giữa hai điểm A và B nên hai tia OA và OB đối nhau (1)
Mà hai tia OM và OB trùng nhau (2)
Từ (1) và (2) => hai tia OA và OM đối nhau.
b) Hai tia OA, OB đối nhau nên ba điểm O, A, B cùng thuộc một đường thẳng
Hai tia OA, OM đối nhau nên ba điểm O, A, M cùng thuộc một đường thẳng
Hai đường thẳng này có hai điểm chung là O và A nên chúng trùng nhau.
Do đó bốn điểm A, B, O, M thẳng hàng.

Ta có hình vẽ như hình bên :
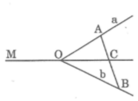
Trong ba tia OA, OM, OB không có tia nào nằm giữa hai tia còn lại.

a: Tia OM cắt đoạn AB tại C
b: Tia OB có cắt AM
c: Tia OA có cắt BM
d: Không có tia nào nằm giữa hai tia còn lại

a) Xét ΔAOB có
Điểm C nằm giữa hai điểm A và B
nên tia OC nằm giữa hai tia OA và OB(Tính chất)
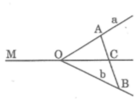
Giải:
Cho hình vẽ như sau:
a) Trên hình, ta thấy OA, OM là hai tia chung gốc, hai tia này tạo thành một đường thẳng.
Vậy OA và OM là hai tia đối nhau.
b) Ta có:
+ Ba điểm A,O,B nằm cùng phía đối với điểm M
+ Ba điểm O,B,M nằm cùng phía đối với điểm A
+ Ba điểm B,M,A nằm cùng phía đối với điểm O
+ Ba điểm M,A,O nằm cùng phía đối với điểm B
Vậy, ta có kết luận: Bốn điểm A,B,O,M là bốn điểm thẳng hàng.