Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Đường thẳng ∆ có vectơ chỉ phương →uu→(1 ; 2 ; 1). H ∈ ∆ nên H(2 + t ; 1 + 2t ; t).
Điểm H ∈ ∆ là hình chiếu vuông góc của A lên ∆ khi và chỉ khi −−→AHAH→ ⊥ →uu→.
Ta có −−→AHAH→(1+t ; 1 + 2t ; t) nên:
−−→AHAH→ ⊥ →uu→ ⇔ →u.−−→AHu→.AH→ = 0.
⇔ 1 + t + 2(1 + 2t) + t = 0
⇔ 6t + 3 = 0 ⇔ t = −12−12.
⇔ H(32;0;−12)H(32;0;−12).
b) Gọi A' là điểm đối xứng của A qua ∆ và H là hình chiếu vuông góc của A lên ∆ thì H là trung điểm của AA'; vì vậy tọa độ của H là trung bình cộng các tọa độ tương ứng của A và A'.
Gọi A'(x ; y ; z) ta có:
x+12=32x+12=32 => x = 2; y = 0; z = -1.
Vậy A'(2 ; 0 ; -1).

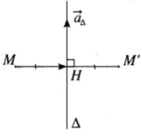
Phương trình tham số của
∆
: 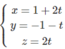
Xét điểm H(1 + 2t; −1 − t; 2t) ∈ ∆
Ta có MH → = (2t − 1; −t; 2t − 1)
a ∆ → = (2; −1; 2)
H là hình chiếu vuông góc của M trên ∆ ⇔ MH → . a ∆ → = 0
⇔ 2(2t − 1) + t + 2(2t − 1) = 0 ⇔ t = 4/9
Ta suy ra tọa độ điểm 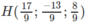

Đáp án A
Xét yếu tố vuông góc nhập
![]()
hoành độ, tung độ, cao độ của các đáp án.
Ta thấy chỉ có đáp án (4; -1; 3) cho kết quả
bằng 0.

Vì A' là điểm đối xứng của A qua ∆ nên H là trung đểm của AA'.
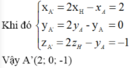

Đáp án D.
![]()
Vì H là hình chiếu vuông góc của A lên đường thẳng ∆
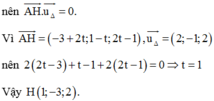

Đáp án D.
Phương pháp giải: Lập phương trình mặt phẳng đi qua điểm và vuông góc với đường thẳng. Khi đó, tọa độ giao điểm của d và (P) chính là tọa độ hình chiếu.
Lời giải: VTCP của đường thẳng d
![]()
Ta có:
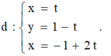
Phương trình mặt phẳng (P) đi qua M, vuông góc với d là :
![]()
![]()
![]()
![]()
![]()
![]()


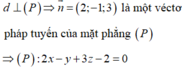
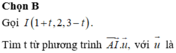
Cho H(2+t;1+2t;t) ∈ ∆ . Ta có: A H → =(1+t;1+2t;t) đường thẳng ∆ có vecto chỉ phương a → =(1;2;1). Vì H là hình chiếu vuông góc của A trên ∆ nên AH vuông góc với ∆ <=> A H → . a → = 0