Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
Gọi:
![]()
Phương trình mặt phẳng (P) có dạng:

Vì M là trực tâm của tam giác ABC nên
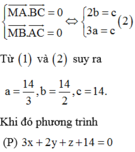

Chọn C
Gọi I là trung điểm của 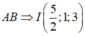
Ta có: ![]()
![]()
IA²+IB² không đổi nên MA²+MB² đạt giá trị nhỏ nhất khi MI đạt giá trị nhỏ nhất.
=> M là hình chiếu của I trên trục Oz.
=> M (0;0;3).

Chọn C
Gọi I là trung điểm của AB 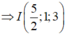
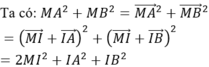
Suy ra: MA2 + MB2 đạt giá trị nhỏ nhất khi MI đạt giá trị nhỏ nhất.
=>M là hình chiếu của I trên trục Oz => M (0 ; 0 ; 3)

Tọa độ trung điểm I của đoạn thẳng AB: \(\left\{{}\begin{matrix}x_I=\dfrac{x_A+x_B}{2}=\dfrac{1+5}{2}=3\\y_I=\dfrac{2+0}{2}=2\\z_I=\dfrac{3-2}{2}=\dfrac{1}{2}\end{matrix}\right.\Rightarrow I\left(3;2;\dfrac{1}{2}\right)\)
Tọa độ trung điểm H của doạn thẳng BC:
\(\left\{{}\begin{matrix}x_H=\dfrac{5-3}{2}=1\\y_H=\dfrac{0+4}{2}=2\\z_H=\dfrac{-2+7}{2}=\dfrac{5}{2}\end{matrix}\right.\Rightarrow H\left(1;2;\dfrac{5}{2}\right)\)
Tọa độ trung điểm K của đoạn thẳng AC:
\(\left\{{}\begin{matrix}x_K=\dfrac{1-3}{2}=-1\\y_K=\dfrac{2+4}{2}=3\\z_H=\dfrac{3+7}{2}=5\end{matrix}\right.\Rightarrow K\left(-1;3;5\right)\)



\(\overrightarrow{OC}=-3i+2j+5k\Rightarrow C\left(-3;2;5\right)\)
\(\left\{{}\begin{matrix}\overrightarrow{AB}=\left(1;8;0\right)\\\overrightarrow{AC}=\left(-4;5;4\right)\end{matrix}\right.\)
Hai vecto \(\overrightarrow{AB};\overrightarrow{AC}\) không cùng phương nên A;B;C tạo thành 1 tam giác
b. Gọi \(E\left(x;y;z\right)\Rightarrow\overrightarrow{BE}=\left(x-2;y-5;z-1\right)\)
\(\overrightarrow{OA}=\left(1;-3;1\right)\) , đồng thời OA=2BE
\(\Rightarrow\left[{}\begin{matrix}\overrightarrow{OA}=2\overrightarrow{BE}\\\overrightarrow{OA}=-2\overrightarrow{BE}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\left(1;-3;1\right)=\left(2x-4;2y-10;2z-2\right)\\\left(1;-3;1\right)=\left(4-2x;10-2y;2-2z\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}E\left(\dfrac{5}{2};\dfrac{7}{2};\dfrac{3}{2}\right)\\E\left(\dfrac{3}{2};\dfrac{13}{2};\dfrac{1}{2}\right)\end{matrix}\right.\)
c.
Gọi \(M\left(x;y;z\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(1;10;0\right)\\\overrightarrow{AM}=\left(x-1;y+3;z-1\right)\\\overrightarrow{CM}=\left(x+3;y-2;z-5\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}3\overrightarrow{AB}=\left(3;30;0\right)\\2\overrightarrow{AM}=\left(2x-2;2y+6;2z-2\right)\\3\overrightarrow{CM}=\left(3x+9;3y-6;3z-15\right)\end{matrix}\right.\)
\(3\overrightarrow{AB}+2\overrightarrow{AM}=3\overrightarrow{CM}\)
\(\Leftrightarrow\left\{{}\begin{matrix}3+2x-2=3x+9\\30+2y+6=3y-6\\0+2z-2=3z-15\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-8\\y=42\\z=13\end{matrix}\right.\)
\(\Rightarrow M\left(-8;42;13\right)\)