Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bo de \(AD.AE=AC^2\) (ban tu chung minh nha , cu tam giac dong dang la ra )
xet \(AD+AE=AD+DH+AD+HE=AH+AD+DH=2AH\)
=> \(\frac{1}{AD}+\frac{1}{AE}=\frac{AD+AE}{AD.AE}=\frac{2AH}{AC^2}\) (1)
ta phai cm \(\frac{2AH}{AC^2}=\frac{2}{AK}\Leftrightarrow AH.AK=AC^2\) (2)
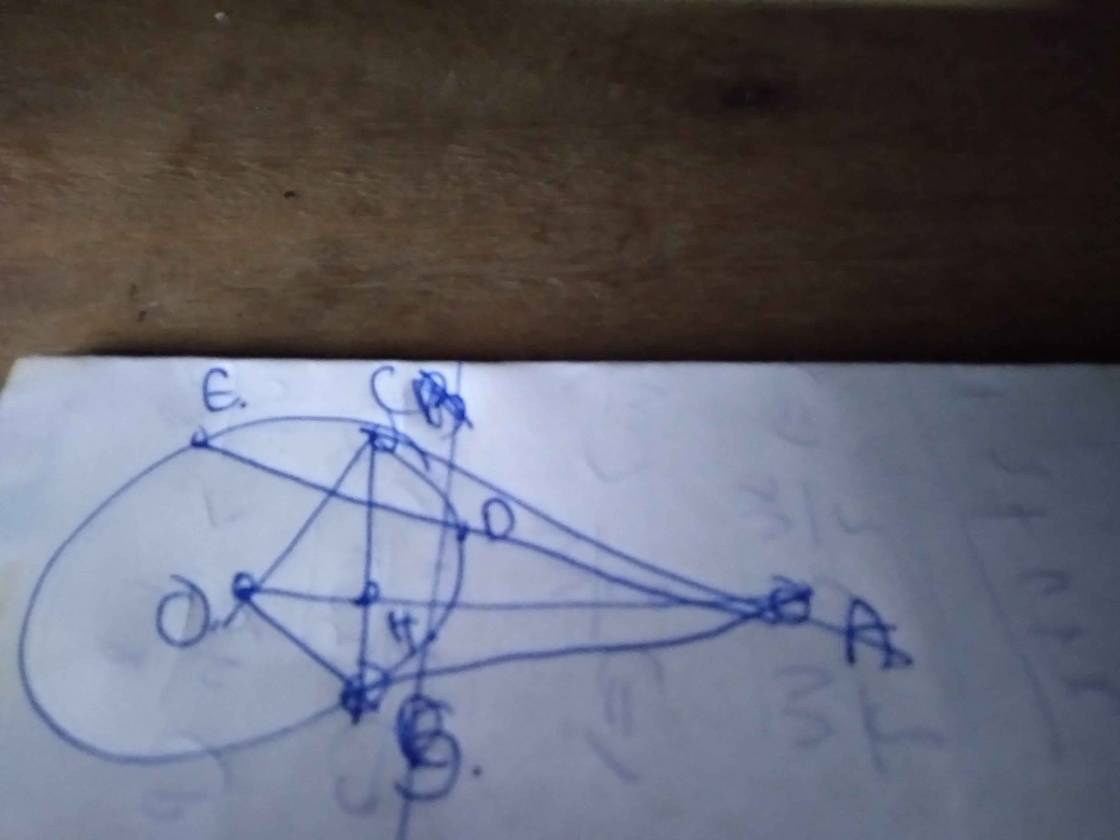
do H la trung diem DE => \(OH\perp DE=>\widehat{ABO}=\widehat{AHO}=\widehat{ACO}=90^0\)
=> A,B,O,H,C thuoc duong tron duong kinh AO
=> \(\widehat{AHC}=\widehat{ABC}\left(\frac{1}{2}sd\widebat{AC}\right)\)
ma \(\widehat{ABC}=\widehat{ACK}\) tinh chat 2 tiep tuyen cat nhau
=> \(\widehat{ACK}=\widehat{AHC}\) lai co \(\widehat{CAK}=\widehat{HAC}\)
=> \(\Delta AKC\approx\Delta ACH\left(g-g\right)\)
=> \(\frac{AK}{AC}=\frac{AC}{AH}\Leftrightarrow AK.AH=AC^2\) (3)
Tu (1),(2),(3) ta co dpcm

a) Xét tứ giác ABOC có
\(\widehat{OBA}+\widehat{OCA}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ABOC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Xét (O) có
AB là tiếp tuyến có B là tiếp điểm(gt)
AC là tiếp tuyến có C là tiếp điểm(gt)
Do đó: AB=AC(Tính chất hai tiếp tuyến cắt nhau)
Ta có: OB=OC(=R)
nên O nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: AB=AC(cmt)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
hay OA\(\perp\)BC
Xét ΔOBC có OB=OC(=R)
nên ΔOBC cân tại O(Định nghĩa tam giác cân)
mà OH là đường cao ứng với cạnh BC
nên H là trung điểm của BC(Đpcm)
sao không có câu B bạn ơi ?? có câu c càng tốt nhưng không làm được thì bỏ qua . nhưng bạn giúp minh câu B với , thankkk

a:Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
hay A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra AO là đường trung trực của BC
b: Xét ΔOBA vuông tại B có BH là đường cao
nên \(BH^2=OH\cdot HA=\left(\dfrac{BC}{2}\right)^2=\dfrac{BC^2}{4}\)

a: Xét tứ giác OIBA có \(\widehat{OIA}=\widehat{OBA}=90^0\)
nên OIBA là tứ giác nội tiếp
b: Xét ΔACD và ΔAEC có
\(\widehat{ACD}=\widehat{AEC}\)
\(\widehat{DAC}\) chung
Do đó: ΔACD\(\sim\)ΔAEC
SUy ra: AC/AE=AD/AC
hay \(AC^2=AE\cdot AD\left(1\right)\)
c: Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
mà OB=OC
nên OA là đường trung trực của BC
Xét ΔOCA vuông tại C có CK là đường cao
nên \(AK\cdot AO=AC^2\left(2\right)\)
Từ (1) và (2) suy ra \(AK\cdot AO=AD\cdot AE\)
hay AK/AE=AD/AO
Xét ΔAKD và ΔAEO có
AK/AE=AD/AO
góc KAD chung
DO đó: ΔAKD\(\sim\)ΔAEO
Suy ra: \(\widehat{AKD}=\widehat{AEO}\)

a) Do H là trung điểm ED nên \(OH⊥DE\) .
Theo tính chất hai tiếp tuyến cắt nhau ta cũng có \(OK⊥DC\)
Vậy thì \(\Delta HOA\sim\Delta IKA\left(g-g\right)\Rightarrow\frac{OA}{OK}=\frac{AH}{AI}\Rightarrow AI.AO=AK.AH\)
b) Ta thấy \(AD.AE=AB^2=AI.AO=AK.AH\)
Vậy nên \(\frac{1}{AD}+\frac{1}{AE}=\frac{AD+AE}{AD.AE}=\frac{AD+AE}{AH.AK}=\frac{2AH}{AH.AK}=\frac{2}{AK}.\)