Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Em tự vẽ đồ thị nhé!
b. Phương trình đường thẳng OA có dạng: \(y=ax\)
Thay tọa độ của A, ta được \(a=1\)
Do \(d//OA\) nên phương trình của \(d\) có dạng: \(y=x+b\)
\(d\) đi qua B nên \(0=2+b\Rightarrow b=-2\)
Suy ra phương trình của \(d\) là: \(y=x-2\)
Phương trình hoành độ giao điểm của \(d\) và \(\left(P\right)\) là:
\(-x^2=x-2\Leftrightarrow x^2+x-2=0\left(1\right)\)
Vì a + b + c = 0 nên (1) có hai nghiệm phân biệt \(x=x_C=1,x=x_D=-2\)
\(\Rightarrow y_C=-1,y_D=-4\)
Ta có: \(x_A=x_C\Rightarrow AC\perp Ox\)
Do đó: \(S_{ACD}=\dfrac{1}{2}\left|x_C-x_D\right|.\left|y_A-y_C\right|=\dfrac{1}{2}\left(x_C-x_D\right)\left(y_A-y_C\right)=3\left(cm^2\right)\)

a: 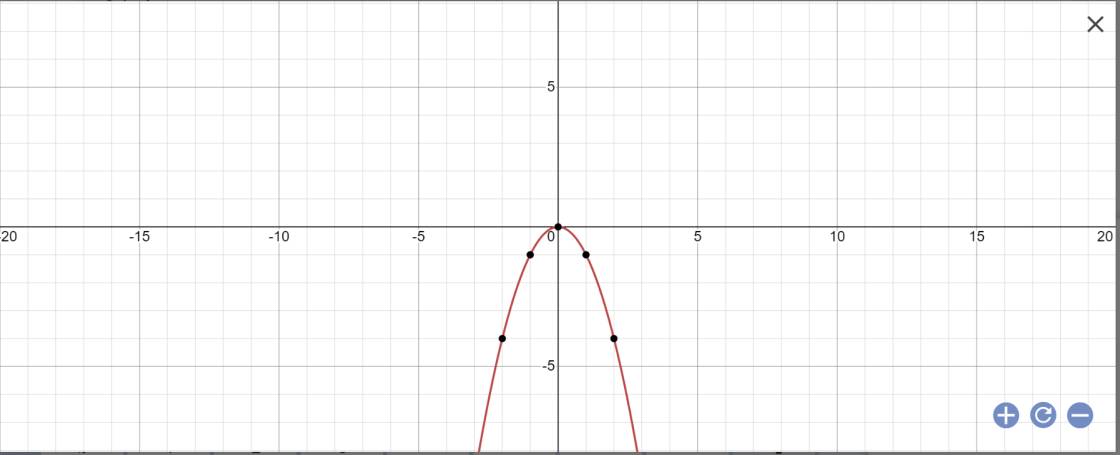
b: Phương trình OA có dạng là y=ax+b
Theo đề, ta có hệ:
0a+b=0 và a+b=1
=>b=0 và a=1
=>y=x
Vì (d)//OA nên (d): y=x+b
Thay x=2 và y=0 vào (d), ta được:
b+2=0
=>b=-2
=>y=x-2
PTHĐGĐ là:
-x^2-x+2=0
vì a*c<0
nên (P) luôn cắt (d) tại hai điểm phân biệt

(a) Sửa đề điểm \(D\left(-3;-2\right)\)
Gọi phương trình đường thẳng \(AB\) là \(\left(d\right):y=ax+b\). Suy ra, giá trị hoành độ và tung độ của \(A,B\) phải thỏa mãn hàm số. Ta sẽ có : \(\left\{{}\begin{matrix}0=a.\left(-2\right)+b\\4=a.0+b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=4\end{matrix}\right.\).
Phương trình đường thẳng \(AB\) là \(\left(d\right):y=2x+4\).
Thay giá trị hoành độ và tung độ của \(D\) vào \(\left(d\right)\Rightarrow-2=2.\left(-3\right)+4\Leftrightarrow-2=-2\) (luôn đúng), do đó \(D\in\left(d\right)\Leftrightarrow A,B,D\) thẳng hàng.
Thay giá trị hoành độ và tung độ của \(C\) vào \(\left(d\right)\Rightarrow1=2.1+4\Leftrightarrow1=6\) (vô lí), do đó \(C\notin\left(d\right)\Leftrightarrow A,B,C\) không thẳng hàng.
(b) Áp dụng công thức khoảng cách giữa hai điểm có tọa độ \(\left(x_1;y_1\right),\left(x_2;y_2\right)\) là : \(d=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\).
Ta suy ra được : \(\left\{{}\begin{matrix}AB=\sqrt{\left(x_A-x_B\right)^2+\left(y_A-y_B\right)^2}\\AC=\sqrt{\left(x_A-x_C\right)^2+\left(y_A-y_B\right)^2}\\BC=\sqrt{\left(x_B-x_C\right)^2+\left(y_B-y_C\right)^2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}AB=\sqrt{\left(-2-0\right)^2+\left(0-4\right)^2}=2\sqrt{5}\\AC=\sqrt{\left(-2-1\right)^2+\left(0-1\right)^2}=\sqrt{10}\\BC=\sqrt{\left(0-1\right)^2+\left(4-1\right)^2}=\sqrt{10}\end{matrix}\right.\).
Ta thấy : \(\left\{{}\begin{matrix}AC^2+BC^2=\left(\sqrt{10}\right)^2+\left(\sqrt{10}\right)^2=20\\AB^2=\left(2\sqrt{5}\right)^2=20\end{matrix}\right.\)
\(\Rightarrow\Delta ABC\) vuông tại \(C\Rightarrow S_{ABC}=\dfrac{1}{2}BC.AC=\dfrac{1}{2}\sqrt{10}\cdot\sqrt{10}=5\left(đvdt\right)\)