Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình tự vẽ nha!
a, Vì tam giác ABC cân tại A
\(\Rightarrow\) \(\widehat{B}=\widehat{C}\) (t/c)
Xét tam giác BHC và tam giác CKB có:
\(\widehat{BCH}=\widehat{CBK}\) (cmt)
\(\widehat{CKB}=\widehat{BHC}=90^o\) (CK và BH là 2 đường cao của tam giác ABC)
BC chung
\(\Rightarrow\) \(\Delta\)BHC = \(\Delta\)CKB (cạnh huyền - góc nhọn)
b, Vì \(\Delta\)BHC = \(\Delta\)CKB (cma)
\(\Rightarrow\) CK = BH (2 cạnh tương ứng)
c, Vì \(\Delta\)BHC = \(\Delta\)CKB (cma)
\(\Rightarrow\) \(\widehat{HBC}=\widehat{KCB}\) (2 góc tương ứng)
Xét tam giác IBC có: \(\widehat{IBC}=\widehat{ICB}\) (cmt)
\(\Rightarrow\) \(\Delta\)IBC cân tại I (định lý tam giác cân)
Chúc bn học tốt!

xét tam giác ABC cân tại A
=> AB=AC(t/c tam giác cân)
=>^ABC=^ACB(t/c tam giác cân)
xét tam giác BAH và tam giác CAK
^A chung
AB=AC(cmt)
^AHB=^AKC
=> tam giác BAH = tam giác CAK(gcg)
=>BH=CK(2 cạnh tương ứng)
=>CH=BK (2 cạnh tương ứng)
b) bạn kiểm tra lại đề bài câu b nhé ! mik chưa thấy dữ kiện nào nói về điểm D cả
c) Ta có : AB=BK+AK
AC=CH+AH
mà AB=AC(cmt);CH=BK(cmt)
=> AK=AH
xét tam giác KAO và tam giác HAO
AK=AH(cmt)
^AKO=^AHO=90o
AO-cạnh chung
=> tam giác KAO = tam giác HAO (ch-cgv)
=>^KAO=^HAO(2 góc tương ứng)
=>^BAI=^CAI
xét tam giác BAI và tam giác CAI
AB=AC(cmt)
^BAI=^CAI(cmt)
AI-cạnh chung
=> tam giác BAI = tam giác CAI
=>^AIB=^AIC ( 2 góc tương ứng)
mà ^AIB+^AIC=180o(kề bù)
=> ^AIB=^AIC=90o
=>AI vuông góc BC
bài 2 bạn tham khảo tại link này
https://h o c 2 4.vn/hoi-dap/question/494804.html
nhớ viết liền từ h o c 2 4 nha! vì olm ko cho viết

Mình xp sửa đề: Chứng minh: ∆BHA = ∆CKA. Từ đó suy ra ∆AHK cân.
`a,`
Xét Tam giác `BHC` và Tam giác `CKA` có:
\(\widehat{A} \) \(\text{chung}\)
\(AB=AC (\text {Tam giác ABC cân tại A})\)
\(\widehat{AHB}=\widehat{AKC}=90^0\)
`=> \text {Tam giác BHA = Tam giác CKA (ch-gn)}`
`-> AH=AK (\text {2 cạnh tương ứng})`
Xét Tam giác `AHK: AH = AK`
`-> \text {Tam giác AHK cân tại A}`
`b,` Vì Tam giác `AHK` cân tại `A ->`\(\widehat{AKH}=\widehat{AHK}\)
`->`\(\widehat{AHK}=\widehat{AKH}=\)\(\dfrac{180-\widehat{A}}{2}\)
Tam giác `ABC` cân tại `A ->`\(\widehat{ABC}=\widehat{ACB}\)
`->`\(\widehat{ABC}=\widehat{ACB}=\)\(\dfrac{180-\widehat{A}}{2}\)
`->`\(\widehat{AKH}=\widehat{ABC}\)
Mà `2` góc này nằm ở vị trí đồng vị
`-> \text {HK // BC (t/c đt' //)}`
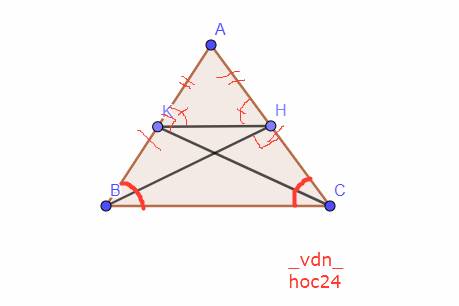

a: Xét ΔAHB vuông ạti H và ΔAKC vuông tại K có
AB=AC
góc BAH chung
=>ΔAHB=ΔAKC
=>AH=AK
b: Xét ΔAKI vuông tại K và ΔAHI vuông tại H co
AI chung
AK=AH
=>ΔAKI=ΔAHI
=>IH=IK
=>AI là trung trực của KI
c: góc EBC+góc ABC=90 độ
góc HBC+góc ACB=90 độ
góc ABC=góc ACB
=>góc EBC=góc HBC
=>BC là phân giác của góc HBE

a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc BAH chung
=>ΔAHB=ΔAKC
=>AH=AK
b: Xet ΔABC có
BH,CK là đường cao
BH cắt CK tại I
=>I là trực tâm
=>AI vuông góc BC tại M
góc KBC+góc ICB=90 độ
góc HCB+góc IBC=90 độ
mà góc KBC=góc HCB
nên góc IBC=góc ICB
=>ΔIBC cân tại I
=>ΔIBC cân tại I
mà IM là đường cao
nên IM là phân giác của góc BIC
c: Xét ΔABC có AK/AB=AH/AC
nên KH//CB

a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc BAH chung
=>ΔAHB=ΔAKC
=>BH=CK
b: Xét ΔAKO vuông tại K và ΔAHO vuông tại H có
AO chung
AK=AH
=>ΔAKO=ΔAHO
=>góc KAO=góc HAO
=>AO là phân giác của góc KAH

a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
\(\widehat{BAH}\) chung
Do đó: ΔAHB=ΔAKC
b: Xét ΔAKD vuông tại K và ΔAHD vuông tại H có
AD chung
AK=AH
Do đó: ΔAKD=ΔAHD
vẽ cả hình giúp mình với
Xét \(\Delta AHB\)và \(\Delta AKC\) có :\(\widehat{AHB}=90^o\)(\(BH⊥AC\))
\(\widehat{AKC}=90^o\)(\(CK⊥AB\))
AB=AC (Tam giác ABC cân tại A)
\(\widehat{KAH}\)là góc chung
Vậy \(\Delta AHB=\Delta AKC\)( cạnh huyền - góc nhọn)
SUy ra AH=AK (ddpcm)